


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-12-2019
Date: 30-7-2020
Date: 4-11-2020
|
A Calkin-Wilf tree is a special type of binary tree obtained by starting with the fraction 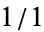 and iteratively adding
and iteratively adding 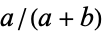 and
and 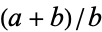 below each fraction
below each fraction 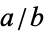 . The Stern-Brocot tree is closely related, putting
. The Stern-Brocot tree is closely related, putting 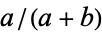 and
and 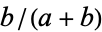 below each fraction
below each fraction 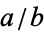 . Both trees generate every rational number. Writing out the terms in sequence gives 1/1, 1/2, 2/1, 1/3, 3/2, 2/3, 3/1, 1/4, 4/3, 3/5, 5/2, 2/5, 5/3, 3/4, 4/1, ...The sequence has the property that each denominator is the next numerator. This sequence, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, ... (OEIS A002487), is known as Stern's diatomic series, or the fusc function (Dijkstra 1982).
. Both trees generate every rational number. Writing out the terms in sequence gives 1/1, 1/2, 2/1, 1/3, 3/2, 2/3, 3/1, 1/4, 4/3, 3/5, 5/2, 2/5, 5/3, 3/4, 4/1, ...The sequence has the property that each denominator is the next numerator. This sequence, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, ... (OEIS A002487), is known as Stern's diatomic series, or the fusc function (Dijkstra 1982).
REFERENCES:
Bogomolny, A. "Fractions on a Binary Tree II." http://www.cut-the-knot.org/blue/Fusc.shtml.
Calkin, N. and Wilf, H. S. "Recounting the Rationals." Amer. Math. Monthly 107, 360-363, 2000.
Dijkstra, E. W. Selected Writings on Computing: A Personal Perspective. New York: Springer-Verlag, pp. 215-232, 1982.
Gibbons, L.; Lester, D.; and Bird, R. "Functional Pearl: Enumerating the Rationals." J. Func. Prog. 16, 281-291, 2006.
Schneider, K. "The Tree of All Fractions." http://demonstrations.wolfram.com/TheTreeOfAllFractions/.
Sloane, N. J. A. Sequence A002487/M0141 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|