


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-3-2019
Date: 25-6-2019
Date: 28-4-2019
|
For 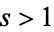 , the Riemann zeta function is given by
, the Riemann zeta function is given by
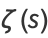 |
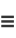 |
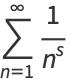 |
(1) |
 |
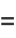 |
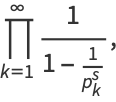 |
(2) |
where 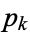 is the
is the 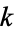 th prime. This is Euler's product (Whittaker and Watson 1990), called by Havil (2003, p. 61) the "all-important formula" and by Derbyshire (2004, pp. 104-106) the "golden key."
th prime. This is Euler's product (Whittaker and Watson 1990), called by Havil (2003, p. 61) the "all-important formula" and by Derbyshire (2004, pp. 104-106) the "golden key."
This can be proved by expanding the product, writing each term as a geometric series, expanding, multiplying, and rearranging terms,
![product_(k=1)^infty1/(1-1/(p_k^s))=1/(1-1/(p_1^s))1/(1-1/(p_2^s))1/(1-1/(p_3^s))...
=[sum_(k=0)^infty(1/(p_1^s))^k][sum_(k=0)^infty(1/(p_2^s))^k][sum_(k=0)^infty(1/(p_3^s))^k]...
=(1+1/(p_1^s)+1/(p_1^(2s))+1/(p_1^(3s))+...)(1+1/(p_2^s)+1/(p_2^(2s))+1/(p_2^(3s))+...)...
=1+sum_(1<=i)1/(p_i^s)+sum_(1<=i<=j)1/(p_i^sp_j^s)+sum_(1<=i<=j<=k)1/(p_i^sp_j^sp_k^s)+...
=1+1/(2^s)+1/(3^s)+1/(4^s)+1/(5^s)+...
=sum_(n=1)^infty1/(n^s)
=zeta(s).](http://mathworld.wolfram.com/images/equations/EulerProduct/NumberedEquation1.gif) |
(3) |
Here, the rearrangement leading to equation (1) follows from the fundamental theorem of arithmetic, since each product of prime powers appears in exactly one denominator and each positive integer equals exactly one product of prime powers.
This product is related to the Möbius function 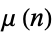 via
via
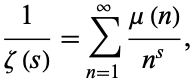 |
(4) |
which can be seen by expanding the product to obtain
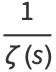 |
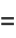 |
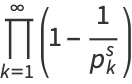 |
(5) |
 |
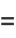 |
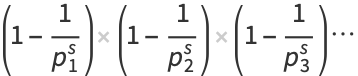 |
(6) |
 |
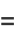 |
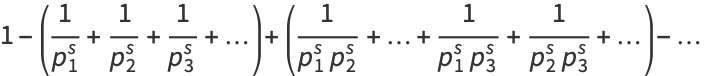 |
(7) |
 |
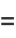 |
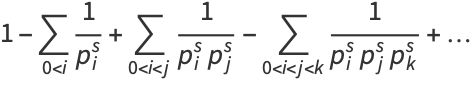 |
(8) |
 |
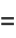 |
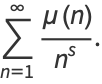 |
(9) |
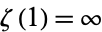 , but the finite product exists, giving
, but the finite product exists, giving
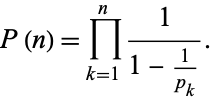 |
(10) |
For upper limits 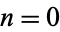 , 1, 2, ..., the products are given by 1, 2, 3, 15/4, 35/8, 77/16, 1001/192, 17017/3072, ... (OEIS A060753 and A038110). Premultiplying by
, 1, 2, ..., the products are given by 1, 2, 3, 15/4, 35/8, 77/16, 1001/192, 17017/3072, ... (OEIS A060753 and A038110). Premultiplying by 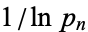 and letting
and letting 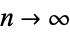 gives a beautiful result known as the Mertens theorem.
gives a beautiful result known as the Mertens theorem.
The Euler product appears briefly in a pan of John Nash's (played by Russell Crowe) blackboard scribblings in Ron Howard's 2001 film A Beautiful Mind.
REFERENCES:
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Edwards, H. M. "The Euler Product Formula." §1.2 in Riemann's Zeta Function. New York: Dover, pp. 6-7, 2001.
Euler, L. "Variae observationes circa series infinitas." St. Petersburg Acad., 1737.
Hardy, G. H. and Wright, E. M. "The Zeta Function." §17.2 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 245-247, 1979.
Havil, J. "The All-Important Formula." §7.1 in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 61-62, 2003.
Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, p. 216, 1996.
Shimura, G. Euler Products and Eisenstein Series. Providence, RI: Amer. Math. Soc., 1997.
Sloane, N. J. A. Sequences A038110 and A060753 in "The On-Line Encyclopedia of Integer Sequences."
Whittaker, E. T. and Watson, G. N. "Euler's Product for 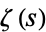 ." §13.3 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 271-272, 1990.
." §13.3 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 271-272, 1990.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|