


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-9-2019
Date: 27-4-2018
Date: 21-9-2018
|
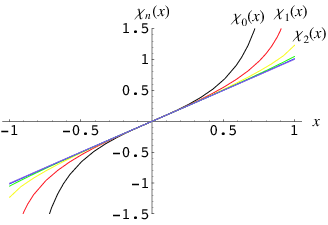
The function defined by
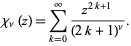 |
(1) |
It is related to the polylogarithm by
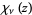 |
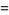 |
![1/2[Li_nu(z)-Li_nu(-z)]](http://mathworld.wolfram.com/images/equations/LegendresChi-Function/Inline3.gif) |
(2) |
 |
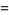 |
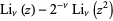 |
(3) |
and to the Lerch transcendent by
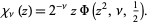 |
(4) |
It takes the special values
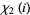 |
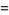 |
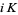 |
(5) |
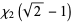 |
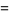 |
![1/(16)pi^2-1/4[ln(sqrt(2)+1)]^2](http://mathworld.wolfram.com/images/equations/LegendresChi-Function/Inline12.gif) |
(6) |
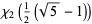 |
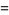 |
![1/(12)pi^2-3/4[ln(1/2(sqrt(5)+1))]^2](http://mathworld.wolfram.com/images/equations/LegendresChi-Function/Inline15.gif) |
(7) |
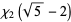 |
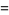 |
![1/(24)pi^2-3/4[ln(1/2(sqrt(5)+1))]^2](http://mathworld.wolfram.com/images/equations/LegendresChi-Function/Inline18.gif) |
(8) |
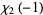 |
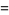 |
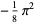 |
(9) |
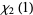 |
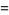 |
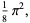 |
(10) |
where i is the imaginary unit and 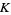 is Catalan's constant (Lewin 1958, p. 19). Other special values include
is Catalan's constant (Lewin 1958, p. 19). Other special values include
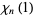 |
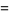 |
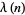 |
(11) |
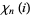 |
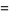 |
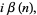 |
(12) |
where 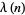 is the Dirichlet lambda function and
is the Dirichlet lambda function and 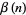 is the Dirichlet beta function.
is the Dirichlet beta function.
REFERENCES:
Cvijović, D. and Klinowski, J. "Closed-Form Summation of Some Trigonometric Series." Math. Comput. 64, 205-210, 1995.
Edwards, J. A Treatise on the Integral Calculus, Vol. 2. New York: Chelsea, p. 290, 1955.
Legendre, A. M. Exercices de calcul intégral, tome 1. p. 247, 1811.
Lewin, L. "Legendre's Chi-Function." §1.8 in Dilogarithms and Associated Functions. London: Macdonald, pp. 17-19, 1958.
Lewin, L. Polylogarithms and Associated Functions. Amsterdam, Netherlands: North-Holland, pp. 282-283, 1981.
Nielsen, N. "Der Eulersche Dilogarithmus und seine Verallgemeinerungen." Nova Acta Leopoldina, Abh. der Kaiserlich Leopoldinisch-Carolinischen Deutschen Akad. der Naturforsch. 90, 121-212, 1909.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|