


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-9-2018
Date: 30-3-2019
Date: 20-6-2019
|
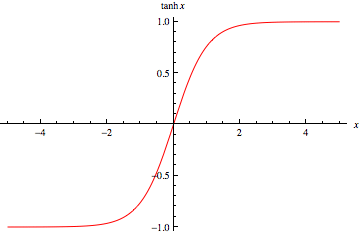 |
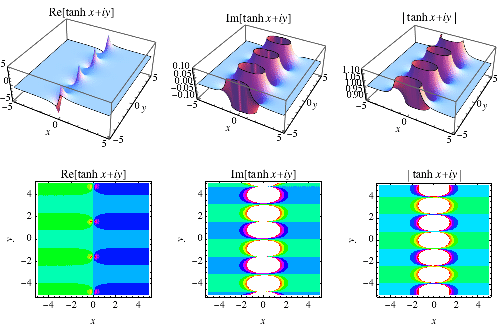 |
By way of analogy with the usual tangent
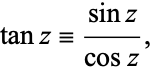 |
(1) |
the hyperbolic tangent is defined as
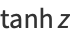 |
 |
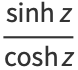 |
(2) |
 |
 |
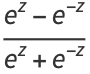 |
(3) |
 |
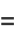 |
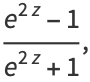 |
(4) |
where 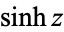 is the hyperbolic sine and
is the hyperbolic sine and 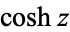 is the hyperbolic cosine. The notation
is the hyperbolic cosine. The notation 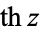 is sometimes also used (Gradshteyn and Ryzhik 2000, p. xxix).
is sometimes also used (Gradshteyn and Ryzhik 2000, p. xxix).
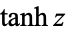 is implemented in the Wolfram Language as Tanh[z].
is implemented in the Wolfram Language as Tanh[z].
Special values include
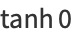 |
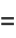 |
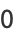 |
(5) |
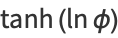 |
 |
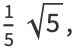 |
(6) |
where 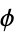 is the golden ratio.
is the golden ratio.
The derivative of 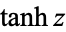 is
is
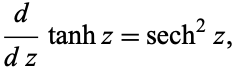 |
(7) |
and higher-order derivatives are given by
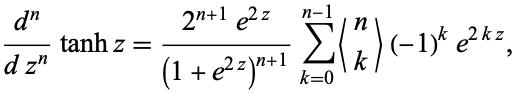 |
(8) |
where  is an Eulerian number.
is an Eulerian number.
The indefinite integral is given by
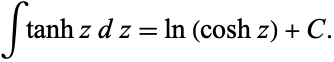 |
(9) |
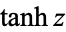 has Taylor series
has Taylor series
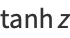 |
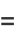 |
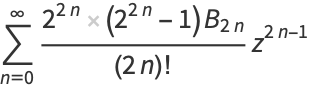 |
(10) |
 |
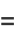 |
 |
(11) |
(OEIS A002430 and A036279).
As Gauss showed in 1812, the hyperbolic tangent can be written using a continued fraction as
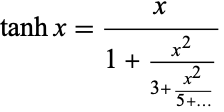 |
(12) |
(Wall 1948, p. 349; Olds 1963, p. 138). This continued fraction is also known as Lambert's continued fraction (Wall 1948, p. 349).
The hyperbolic tangent 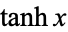 satisfies the second-order ordinary differential equation
satisfies the second-order ordinary differential equation
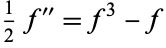 |
(13) |
together with the boundary conditions 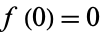 and
and 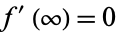 .
.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Hyperbolic Functions." §4.5 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 83-86, 1972.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Jeffrey, A. "Hyperbolic Identities." §2.5 in Handbook of Mathematical Formulas and Integrals, 2nd ed. Orlando, FL: Academic Press, pp. 117-122, 2000.
Olds, C. D. Continued Fractions. New York: Random House, 1963.
Sloane, N. J. A. Sequences A002430/M2100 and A036279 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Hyperbolic Tangent 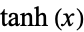 and Cotangent
and Cotangent 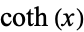 Functions." Ch. 30 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 279-284, 1987.
Functions." Ch. 30 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 279-284, 1987.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
Zwillinger, D. (Ed.). "Hyperbolic Functions." §6.7 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 476-481 1995.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|