


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-8-2019
Date: 4-9-2019
Date: 3-6-2019
|
Stirling's approximation gives an approximate value for the factorial function 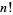 or the gamma function
or the gamma function 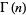 for
for 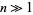 . The approximation can most simply be derived for
. The approximation can most simply be derived for 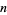 an integer by approximating the sum over the terms of the factorial with an integral, so that
an integer by approximating the sum over the terms of the factorial with an integral, so that
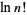 |
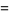 |
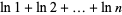 |
(1) |
 |
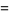 |
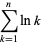 |
(2) |
 |
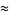 |
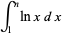 |
(3) |
 |
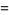 |
![[xlnx-x]_1^n](http://mathworld.wolfram.com/images/equations/StirlingsApproximation/Inline16.gif) |
(4) |
 |
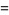 |
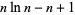 |
(5) |
 |
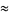 |
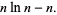 |
(6) |
The equation can also be derived using the integral definition of the factorial,
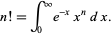 |
(7) |
Note that the derivative of the logarithm of the integrand can be written
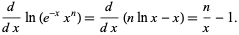 |
(8) |
The integrand is sharply peaked with the contribution important only near 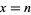 . Therefore, let
. Therefore, let 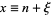 where
where 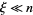 , and write
, and write
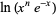 |
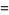 |
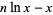 |
(9) |
 |
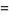 |
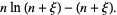 |
(10) |
Now,
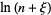 |
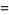 |
![ln[n(1+xi/n)]](http://mathworld.wolfram.com/images/equations/StirlingsApproximation/Inline34.gif) |
(11) |
 |
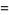 |
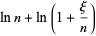 |
(12) |
 |
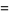 |
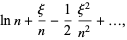 |
(13) |
so
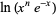 |
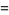 |
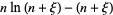 |
(14) |
 |
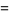 |
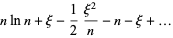 |
(15) |
 |
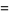 |
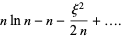 |
(16) |
Taking the exponential of each side then gives
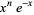 |
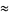 |
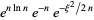 |
(17) |
 |
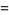 |
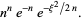 |
(18) |
Plugging into the integral expression for 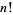 then gives
then gives
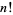 |
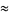 |
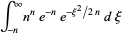 |
(19) |
 |
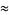 |
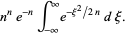 |
(20) |
Evaluating the integral gives
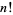 |
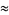 |
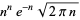 |
(21) |
 |
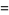 |
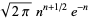 |
(22) |
(Wells 1986, p. 45). Taking the logarithm of both sides then gives
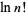 |
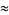 |
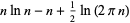 |
(23) |
 |
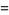 |
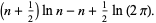 |
(24) |
This is Stirling's series with only the first term retained and, for large 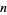 , it reduces to Stirling's approximation
, it reduces to Stirling's approximation
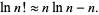 |
(25) |
Taking successive terms of 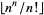 , where
, where 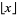 is the floor function, gives the sequence 1, 2, 4, 10, 26, 64, 163, 416, 1067, 2755, ... (OEIS A055775).
is the floor function, gives the sequence 1, 2, 4, 10, 26, 64, 163, 416, 1067, 2755, ... (OEIS A055775).
Stirling's approximation can be extended to the double inequality
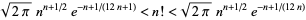 |
(26) |
(Robbins 1955, Feller 1968).
Gosper has noted that a better approximation to 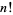 (i.e., one which approximates the terms in Stirling's series instead of truncating them) is given by
(i.e., one which approximates the terms in Stirling's series instead of truncating them) is given by
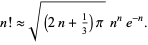 |
(27) |
Considering 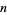 a real number so that
a real number so that 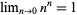 , the equation (27) also gives a much closer approximation to the factorial of 0,
, the equation (27) also gives a much closer approximation to the factorial of 0, 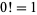 , yielding
, yielding 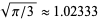 instead of 0 obtained with the conventional Stirling approximation.
instead of 0 obtained with the conventional Stirling approximation.
REFERENCES:
Feller, W. "Stirling's Formula." §2.9 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 50-53, 1968.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 86-88, 2003.
Robbins, H. "A Remark of Stirling's Formula." Amer. Math. Monthly 62, 26-29, 1955.
Sloane, N. J. A. Sequence A055775 in "The On-Line Encyclopedia of Integer Sequences."
Stirling, J. Methodus differentialis, sive tractatus de summation et interpolation serierum infinitarium. London, 1730. English translation by Holliday, J. The Differential Method: A Treatise of the Summation and Interpolation of Infinite Series. 1749.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 45, 1986.
Whittaker, E. T. and Robinson, G. "Stirling's Approximation to the Factorial." §70 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 138-140, 1967.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|