Mu Function

There are two functions commonly denoted 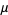, each of which is defined in terms of integrals. Another unrelated mathematical function represented using the Greek letter  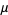is the Möbius function.

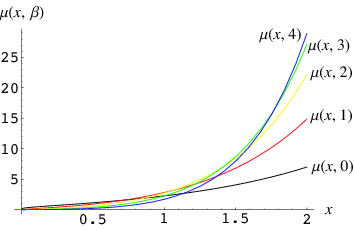
The two-argument 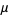-function is defined by the definite integral

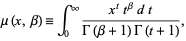where 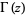 is the gamma function (Erdélyi et al. 1981a, p. 388; Prudnikov et al. 1990, p. 798; Gradshteyn and Ryzhik 2000, p. 1109), while the three-argument 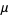-function is defined by

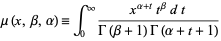(Prudnikov et al. 1990, p. 798; Gradshteyn and Ryzhik 2000, p. 1109).

REFERENCES:

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 388, 1981a.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Ch. 18 in Higher Transcendental Functions, Vol. 3. New York: Krieger, p. 217, 1981b.

Gradshteyn, I. S. and Ryzhik, I. M. "The Functions 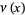, , 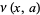, , 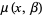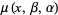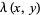." §9.64 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1109, 2000.

Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, 1990.