
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-8-2018
Date: 10-6-2019
Date: 9-8-2019
|
The second fundamental theorem of calculus holds for 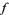 a continuous function on an open interval
a continuous function on an open interval 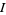 and
and 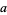 any point in
any point in 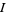 , and states that if
, and states that if 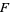 is defined by the integral (antiderivative)
is defined by the integral (antiderivative)
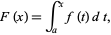 |
then
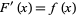 |
at each point in 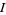 , where
, where 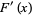 is the derivative of
is the derivative of 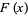 .
.
REFERENCES:
Anton, H. "The Second Fundamental Theorem of Calculus." §5.10 in Calculus: A New Horizon, 6th ed. New York: Wiley, pp. 345-348, 1999.
Apostol, T. M. "Primitive Functions and the Second Fundamental Theorem of Calculus." §5.3 in Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 205-207, 1967.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|