المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Racah V-Coefficient |
 1639
 01:23 صباحاً
date: 16-4-2019 |
Author : Biedenharn, L. C. and Louck, J. D 
Book or Source : The Racah-Wigner Algebra in Quantum Theory. Reading, MA: Addison-Wesley, 1981. 
Page and Part : ...|
Read More
Date: 21-7-2019
1494
Date: 21-7-2019
1538
Date: 21-9-2019
1650
|
The Racah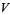 
-coefficients are written
 |
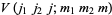(1) |
and are sometimes expressed using the related Clebsch-Gordan coefficients
 |
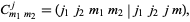(2) |
or Wigner 3j-symbols. Connections among the three are
 |
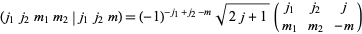(3) |
 |
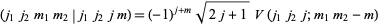(4) |
 |
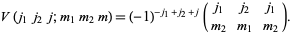(5) |
REFERENCES:
Biedenharn, L. C. and Louck, J. D. The Racah-Wigner Algebra in Quantum Theory. Reading, MA: Addison-Wesley, 1981.
Biedenharn, L. C. and Louck, J. D. Angular Momentum in Quantum Physics: Theory and Applications. Reading, MA: Addison-Wesley, 1981.
Sobel'man, I. I. "Angular Momenta." Ch. 4 in Atomic Spectra and Radiative Transitions, 2nd ed. Berlin: Springer-Verlag, 1992.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
