المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Separation Theorem |
 1014
 01:59 مساءً
date: 11-3-2019 |
Author : Szegö, G 
Book or Source : Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc. 
Page and Part : p. 50|
Read More
Date: 6-3-2017
1972
Date: 6-3-2017
1329
Date: 19-1-2019
875
|
There exist numbers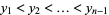 
, 
, 
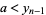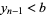, such that
 |
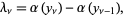(1) |
where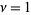 
, 2, ..., 
, 
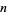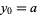and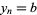 
. Furthermore, the zeros 
, ..., 
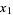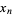, arranged in increasing order, alternate with the numbers 
, ...
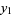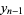, so
 |
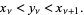(2) |
More precisely,
 |
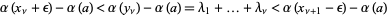(3) |
for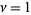 
, ..., 
.
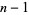REFERENCES:
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., p. 50, 1975.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
