


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-1-2019
Date: 19-1-2019
Date: 23-2-2019
|
Let 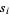 be the sum of the products of distinct polynomial roots
be the sum of the products of distinct polynomial roots 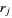 of the polynomial equation of degree
of the polynomial equation of degree 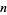
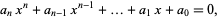 |
(1) |
where the roots are taken 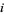 at a time (i.e.,
at a time (i.e., 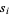 is defined as the symmetric polynomial
is defined as the symmetric polynomial 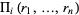 )
) 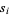 is defined for
is defined for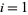 , ...,
, ..., 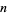 . For example, the first few values of
. For example, the first few values of 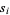 are
are
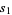 |
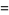 |
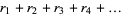 |
(2) |
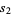 |
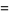 |
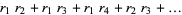 |
(3) |
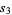 |
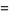 |
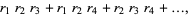 |
(4) |
and so on. Then Vieta's formulas states that
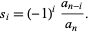 |
(5) |
The theorem was proved by Viète (also known as Vieta, 1579) for positive roots only, and the general theorem was proved by Girard.
This can be seen for a second-degree polynomial by multiplying out,
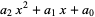 |
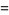 |
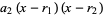 |
(6) |
 |
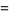 |
![a_2[x^2-(r_1+r_2)x+r_1r_2],](http://mathworld.wolfram.com/images/equations/VietasFormulas/Inline25.gif) |
(7) |
so
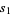 |
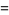 |
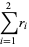 |
(8) |
 |
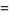 |
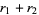 |
(9) |
 |
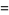 |
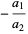 |
(10) |
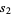 |
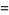 |
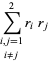 |
(11) |
 |
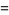 |
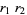 |
(12) |
 |
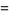 |
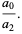 |
(13) |
Similarly, for a third-degree polynomial,
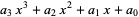 |
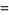 |
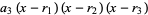 |
(14) |
 |
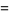 |
![a_3[x^3-(r_1+r_2+r_3)x^2+(r_1r_2+r_1r_3+r_2r_3)x-r_1r_2r_3],](http://mathworld.wolfram.com/images/equations/VietasFormulas/Inline49.gif) |
(15) |
so
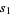 |
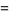 |
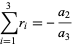 |
(16) |
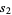 |
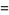 |
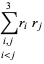 |
(17) |
 |
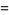 |
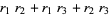 |
(18) |
 |
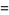 |
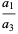 |
(19) |
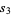 |
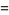 |
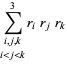 |
(20) |
 |
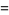 |
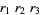 |
(21) |
 |
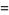 |
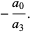 |
(22) |
REFERENCES:
Bold, B. Famous Problems of Geometry and How to Solve Them. New York: Dover, p. 56, 1982.
Borwein, P. and Erdélyi, T. "Newton's Identities." §1.1.E.2 in Polynomials and Polynomial Inequalities. New York: Springer-Verlag, pp. 5-6, 1995.
Coolidge, J. L. A Treatise on Algebraic Plane Curves. New York: Dover, pp. 1-2, 1959.
Girard, A. Invention nouvelle en l'algèbre. Leiden, Netherlands: Bierens de Haan, 1884.
Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia," Vol. 9. Dordrecht, Netherlands: Reidel, p. 416, 1988.
van der Waerden, B. L. Algebra, Vol. 1. New York: Springer-Verlag, 1993.
Viète, F. Opera mathematica. 1579. Reprinted Leiden, Netherlands, 1646.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
ضمن مؤتمر ذاكرة الألم في العراق مدير كرسي اليونسكو في جامعة الموصل يقدّم دراسةً تناقش استراتيجية الكرسي لنبذ التطرف وتعزيز ثقافة السلام
|
|
|