المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Rényi,s Polynomial |
 512
 02:55 مساءً
date: 23-2-2019 |
Author : Coppersmith, D. and Davenport, J 
Book or Source : "Polynomials Whose Powers Are Sparse." Acta Arith. 58, 
Page and Part : ...|
Read More
Date: 23-2-2019
998
Date: 13-2-2019
754
Date: 4-3-2019
986
|
Rényi's polynomial is the polynomial
 |
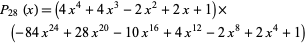(Rényi 1947, Coppersmith and Davenport 1991) that has 29 terms and whose square has 28, making it a sparse polynomial square.
REFERENCES:
Coppersmith, D. and Davenport, J. "Polynomials Whose Powers Are Sparse." Acta Arith. 58, 79-87, 1991.
Rényi, A. "On the Minimal Number of Terms in the Square of a Polynomial." Acta Math. Hungar. 1, 30-34, 1947. Reprinted in Selected Papers of Alfred Rényi, Vol. 1. Budapest, pp. 44-47, 1976.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|
