Bring-Jerrard Quintic Form

A Tschirnhausen transformation can be used to algebraically transform a general quintic equation to the form

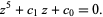(1)

In practice, the general quintic is first reduced to the principal quintic form

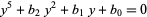(2)

before the transformation is done. Then, we require that the sum of the third powers of the roots vanishes, so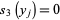. We assume that the roots  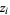of the Bring-Jerrard quintic are related to the roots  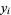of the principal quintic form by

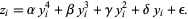(3)

In a similar manner to the principal quintic form transformation, we can express the coefficients 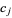 in terms of the .

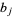REFERENCES:

Grunert, J. A. "VIII. Miscellen von dem Herausgeber." Archiv der Math. Phys. 41, 105-112, 1864.

Klein, F. "Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades." Math. Ann.14, 111-172, 1878-79.

Tortolini, B. "Rivista bibliografica sopra a transformazione del Sig. Jerrard per l'equazioni di quinto grado." Annali di Mat. pura appl. 6, 33-42, 1864.