


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-3-2017
Date: 13-2-2019
Date: 23-1-2019
|
Let 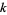 be a field of finite characteristic
be a field of finite characteristic 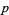 . Then a polynomial
. Then a polynomial ![P(x) in k[x]](http://mathworld.wolfram.com/images/equations/AdditivePolynomial/Inline3.gif) is said to be additive iff
is said to be additive iff 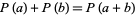 for
for 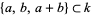 . For example,
. For example, 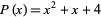 is additive for
is additive for 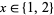 , since
, since
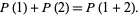 |
A more interesting class of additive polynomials known as absolutely additive polynomials are defined on an algebraic closure 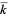 of
of 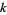 . For example, for any such
. For example, for any such 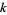 ,
, 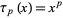 is an absolutely additive polynomial, since
is an absolutely additive polynomial, since 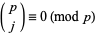 , for
, for 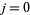 , ...,
, ..., 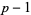 . The polynomial
. The polynomial 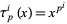 is also absolutely additive.
is also absolutely additive.
Let the ring of polynomials spanned by linear combinations of 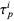 be denoted
be denoted 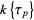 . If
. If 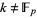 , then
, then 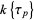 is not commutative.
is not commutative.
Not all additive polynomials are in 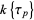 . In particular, if
. In particular, if 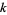 is an infinite field, then a polynomial
is an infinite field, then a polynomial ![P(x) in k[x]](http://mathworld.wolfram.com/images/equations/AdditivePolynomial/Inline22.gif) is additive iff
is additive iff 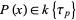 . For
. For 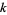 be a finite field of characteristic
be a finite field of characteristic 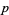 , the set of absolutely additive polynomials over
, the set of absolutely additive polynomials over 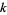 equals
equals 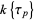 , so the qualification "absolutely" can be dropped and the term "additive" alone can be used to refer to an element of
, so the qualification "absolutely" can be dropped and the term "additive" alone can be used to refer to an element of 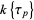 .
.
If 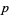 is a fixed power
is a fixed power 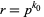 and
and 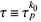 , then
, then 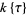 is a ring of polynomials in
is a ring of polynomials in  . Moreover, if
. Moreover, if 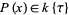 , then
, then 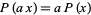 for all
for all 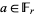 . In this case,
. In this case, 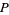 is said to be a
is said to be a 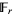 -linear polynomial.
-linear polynomial.
The fundamental theorem of additive polynomials states that if ![P(x) in k[x]](http://mathworld.wolfram.com/images/equations/AdditivePolynomial/Inline39.gif) is a separable polynomial and
is a separable polynomial and 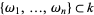 is the set of its roots, then
is the set of its roots, then 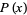 is additive iff if
is additive iff if 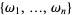 is a subgroup.
is a subgroup.
It therefore follows as a corollary that such a polynomial 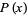 is
is 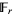 -linear iff its roots form a
-linear iff its roots form a 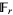 -vector subspace of
-vector subspace of 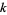 .
.
REFERENCES:
Goss, D. Basic Structures of Function Field Arithmetic. Berlin: Springer-Verlag, pp. 1-33, 1996.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
العتبة الحسينية تطلق فعاليات المخيم القرآني الثالث في جامعة البصرة
|
|
|