


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-7-2018
Date: 13-6-2018
Date: 30-12-2018
|
Poisson's equation is
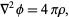 |
(1) |
where 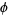 is often called a potential function and
is often called a potential function and 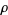 a density function, so the differential operator in this case is
a density function, so the differential operator in this case is 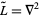 . As usual, we are looking for a Green's function
. As usual, we are looking for a Green's function 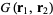 such that
such that
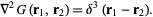 |
(2) |
But from Laplacian,
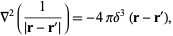 |
(3) |
so
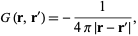 |
(4) |
and the solution is
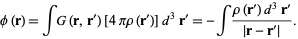 |
(5) |
Expanding 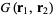 in the spherical harmonics
in the spherical harmonics 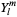 gives
gives
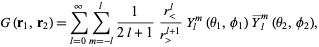 |
(6) |
where 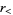 and
and 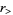 are greater than/less than symbols. this expression simplifies to
are greater than/less than symbols. this expression simplifies to
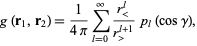 |
(7) |
where 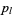 are Legendre polynomials, and
are Legendre polynomials, and 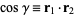 . Equations (6) and (7) give the addition theorem for Legendre polynomials.
. Equations (6) and (7) give the addition theorem for Legendre polynomials.
In cylindrical coordinates, the Green's function is much more complicated,
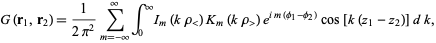 |
(8) |
where 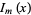 and
and 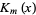 are modified Bessel functions of the first and second kinds (Arfken 1985).
are modified Bessel functions of the first and second kinds (Arfken 1985).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 485-486, 905, and 912, 1985.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|