Erf

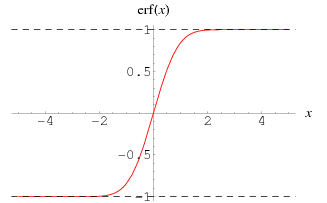
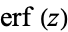 is the "error function" encountered in integrating the normal distribution (which is a normalized form of the Gaussian function). It is an entire functiondefined by

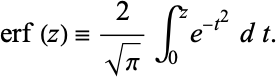(1)

Note that some authors (e.g., Whittaker and Watson 1990, p. 341) define 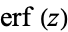 without the leading factor of .

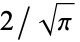Erf is implemented in the Wolfram Language as Erf[z]. A two-argument form giving 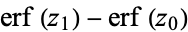 is also implemented as Erf[z0, z1].

Erf satisfies the identities

			(2)
			(3)
			(4)

where 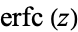 is erfc, the complementary error function, and  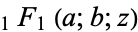is a confluent hypergeometric function of the first kind. For ,

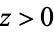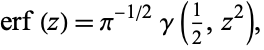(5)

where 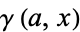 is the incomplete gamma function.

Erf can also be defined as a Maclaurin series

			(6)
			(7)

(OEIS A007680). Similarly,

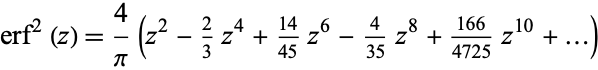(8)

(OEIS A103979 and A103980).

For 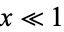,  may be computed from

			(9)
			(10)

(OEIS A000079 and A001147; Acton 1990).

For ,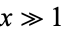

			(11)
			(12)

Using integration by parts gives

			(13)
			(14)
			(15)
			(16)

so

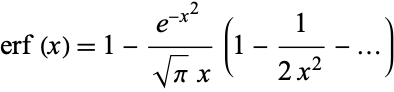(17)

and continuing the procedure gives the asymptotic series

			(18)
			(19)
			(20)

(OEIS A001147 and A000079).

Erf has the values

			(21)
			(22)

It is an odd function

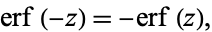(23)

and satisfies

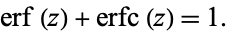(24)

Erf may be expressed in terms of a confluent hypergeometric function of the first kind  as

			(25)
			(26)

Its derivative is

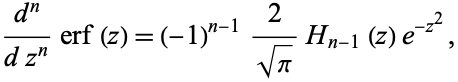(27)

where 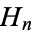 is a Hermite polynomial. The first derivative is

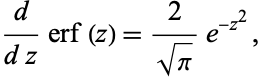(28)

and the integral is

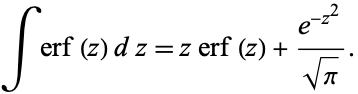(29)

Min   Max       Re       Im

Erf can also be extended to the complex plane, as illustrated above.

A simple integral involving erf that Wolfram Language cannot do is given by

(30)

(M. R. D'Orsogna, pers. comm., May 9, 2004). More complicated integrals include

(31)

(M. R. D'Orsogna, pers. comm., Dec. 15, 2005).

Erf has the continued fraction

			(32)
			(33)

(Wall 1948, p. 357), first stated by Laplace in 1805 and Legendre in 1826 (Olds 1963, p. 139), proved by Jacobi, and rediscovered by Ramanujan (Watson 1928; Hardy 1999, pp. 8-9).

Definite integrals involving 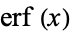 include Definite integrals involving  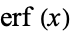include

			(34)
			(35)
			(36)
			(37)
			(38)

The first two of these appear in Prudnikov et al. (1990, p. 123, eqns. 2.8.19.8 and 2.8.19.11), with , .

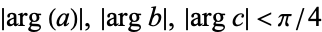A complex generalization of 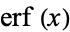 is defined as

			(39)
			(40)

Integral representations valid only in the upper half-plane  are given by

			(41)
			(42)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Error Function and Fresnel Integrals." Ch. 7 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 297-309, 1972.

Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., p. 16, 1990.

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 568-569, 1985.

Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 105, 2003.

Olds, C. D. Continued Fractions. New York: Random House, 1963.

Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 2: Special Functions. New York: Gordon and Breach, 1990.

Sloane, N. J. A. Sequences A000079/M1129, A001147/M3002, A007680/M2861, A103979, A103980 in "The On-Line Encyclopedia of Integer Sequences."

Spanier, J. and Oldham, K. B. "The Error Function 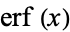 and Its Complement 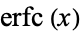." Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.

Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.

Watson, G. N. "Theorems Stated by Ramanujan (IV): Theorems on Approximate Integration and Summation of Series." J. London Math. Soc. 3, 282-289, 1928.

Whittaker, E. T. and Robinson, G. "The Error Function." §92 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 179-182, 1967.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.