


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-11-2018
Date: 18-11-2018
Date: 27-11-2018
|
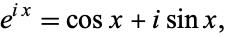 |
(1) |
where i is the imaginary unit. Note that Euler's polyhedral formula is sometimes also called the Euler formula, as is the Euler curvature formula. The equivalent expression
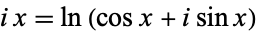 |
(2) |
had previously been published by Cotes (1714).
The special case of the formula with 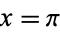 gives the beautiful identity
gives the beautiful identity
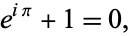 |
(3) |
an equation connecting the fundamental numbers i, pi, e, 1, and 0 (zero), the fundamental operations 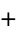 ,
, 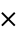 , and exponentiation, the most important relation
, and exponentiation, the most important relation 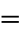 , and nothing else. Gauss is reported to have commented that if this formula was not immediately obvious, the reader would never be a first-class mathematician (Derbyshire 2004, p. 202).
, and nothing else. Gauss is reported to have commented that if this formula was not immediately obvious, the reader would never be a first-class mathematician (Derbyshire 2004, p. 202).
The Euler formula can be demonstrated using a series expansion
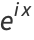 |
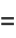 |
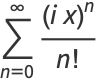 |
(4) |
 |
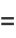 |
 |
(5) |
 |
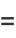 |
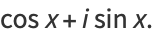 |
(6) |
It can also be demonstrated using a complex integral. Let
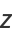 |
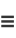 |
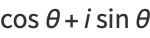 |
(7) |
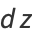 |
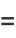 |
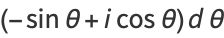 |
(8) |
 |
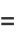 |
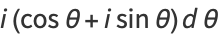 |
(9) |
 |
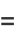 |
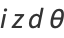 |
(10) |
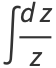 |
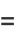 |
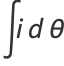 |
(11) |
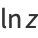 |
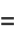 |
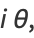 |
(12) |
so
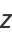 |
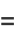 |
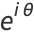 |
(13) |
 |
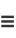 |
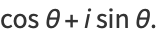 |
(14) |
A mathematical joke asks, "How many mathematicians does it take to change a light bulb?" and answers "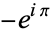 " (which, of course, equals 1).
" (which, of course, equals 1).
REFERENCES:
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. "Euler's Wonderful Relation." The Book of Numbers. New York: Springer-Verlag, pp. 254-256, 1996.
Cotes, R. "Logometria." Philos. Trans. Roy. Soc. London 29, 5-45, 1714.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Euler, L. "De summis serierum reciprocarum ex potestatibus numerorum naturalium ortarum dissertatio altera." Miscellanea Berolinensia 7, 172-192, 1743.
Euler, L. Introductio in Analysin Infinitorum, Vol. 1. Bosquet, Lucerne, Switzerland: p. 104, 1748.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, p. 212, 1998.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|