

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Complex Number
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover,
الجزء والصفحة:
...
18-10-2018
5629
Complex Number
The complex numbers are the field 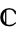 of numbers of the form
of numbers of the form 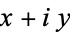 , where
, where 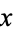 and
and 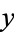 are real numbers and i is the imaginary unit equal to the square root of
are real numbers and i is the imaginary unit equal to the square root of 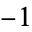 ,
, 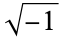 . When a single letter
. When a single letter 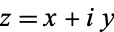 is used to denote a complex number, it is sometimes called an "affix." In component notation,
is used to denote a complex number, it is sometimes called an "affix." In component notation, 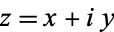 can be written
can be written 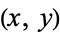 . The field of complex numbers includes the field of real numbers as a subfield.
. The field of complex numbers includes the field of real numbers as a subfield.
The set of complex numbers is implemented in the Wolfram Language as Complexes. A number 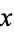 can then be tested to see if it is complex using the command Element[x, Complexes], and expressions that are complex numbers have the Head of Complex.
can then be tested to see if it is complex using the command Element[x, Complexes], and expressions that are complex numbers have the Head of Complex.
Complex numbers are useful abstract quantities that can be used in calculations and result in physically meaningful solutions. However, recognition of this fact is one that took a long time for mathematicians to accept. For example, John Wallis wrote, "These Imaginary Quantities (as they are commonly called) arising from the Supposed Root of a Negative Square (when they happen) are reputed to imply that the Case proposed is Impossible" (Wells 1986, p. 22).
Through the Euler formula, a complex number
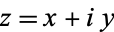 |
(1) |
may be written in "phasor" form
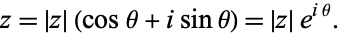 |
(2) |
Here, 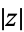 is known as the complex modulus (or sometimes the complex norm) and
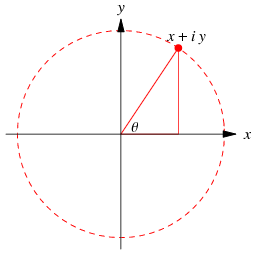
is known as the complex modulus (or sometimes the complex norm) and 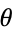 is known as the complex argument or phase. The plot above shows what is known as an Argand diagram of the point
is known as the complex argument or phase. The plot above shows what is known as an Argand diagram of the point 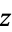 , where the dashed circle represents the complex modulus
, where the dashed circle represents the complex modulus 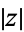 of
of 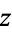 and the angle
and the angle 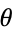 represents its complex argument. Historically, the geometric representation of a complex number as simply a point in the plane was important because it made the whole idea of a complex number more acceptable. In particular, "imaginary" numbers became accepted partly through their visualization.
represents its complex argument. Historically, the geometric representation of a complex number as simply a point in the plane was important because it made the whole idea of a complex number more acceptable. In particular, "imaginary" numbers became accepted partly through their visualization.
Unlike real numbers, complex numbers do not have a natural ordering, so there is no analog of complex-valued inequalities. This property is not so surprising however when they are viewed as being elements in the complex plane, since points in a plane also lack a natural ordering.
The absolute square of 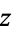 is defined by
is defined by 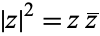 , with
, with 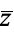 the complex conjugate, and the argument may be computed from
the complex conjugate, and the argument may be computed from
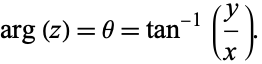 |
(3) |
The real 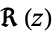 and imaginary parts
and imaginary parts 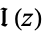 are given by
are given by
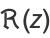 |
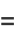 |
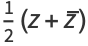 |
(4) |
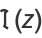 |
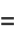 |
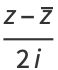 |
(5) |
 |
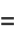 |
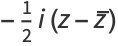 |
(6) |
 |
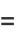 |
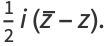 |
(7) |
de Moivre's identity relates powers of complex numbers for real 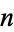 by
by
![z^n=|z|^n[cos(ntheta)+isin(ntheta)].](http://mathworld.wolfram.com/images/equations/ComplexNumber/NumberedEquation4.gif) |
(8) |
A power of complex number 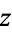 to a positive integer exponent
to a positive integer exponent 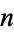 can be written in closed form as
can be written in closed form as
![z^n=[x^n-(n; 2)x^(n-2)y^2+(n; 4)x^(n-4)y^4-...]
+i[(n; 1)x^(n-1)y-(n; 3)x^(n-3)y^3+...].](http://mathworld.wolfram.com/images/equations/ComplexNumber/NumberedEquation5.gif) |
(9) |
The first few are explicitly
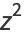 |
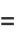 |
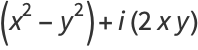 |
(10) |
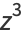 |
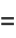 |
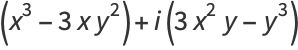 |
(11) |
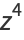 |
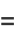 |
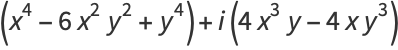 |
(12) |
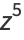 |
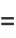 |
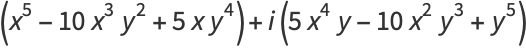 |
(13) |
(Abramowitz and Stegun 1972).
Complex addition
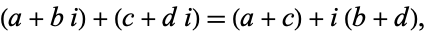 |
(14) |
complex subtraction
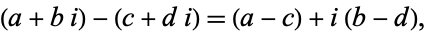 |
(15) |
complex multiplication
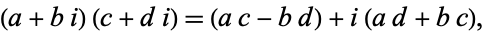 |
(16) |
and complex division
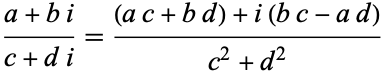 |
(17) |
can also be defined for complex numbers. Complex numbers may also be taken to complex powers. For example, complex exponentiation obeys
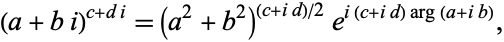 |
(18) |
where 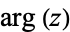 is the complex argument.
is the complex argument.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 16-17, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 353-357, 1985.
Bold, B. "Complex Numbers." Ch. 3 in Famous Problems of Geometry and How to Solve Them. New York: Dover, pp. 19-27, 1982.
Courant, R. and Robbins, H. "Complex Numbers." §2.5 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 88-103, 1996.
Ebbinghaus, H. D.; Hirzebruch, F.; Hermes, H.; Prestel, A; Koecher, M.; Mainzer, M.; and Remmert, R. Numbers. New York: Springer-Verlag, 1990.
Krantz, S. G. "Complex Arithmetic." §1.1 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 1-7, 1999.
Mazur, B. Imagining Numbers (Particularly the Square Root of Minus Fifteen). Farrar, Straus and Giroux, 2003.
Morse, P. M. and Feshbach, H. "Complex Numbers and Variables." §4.1 in Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 349-356, 1953.
Nahin, P. J. An Imaginary Tale: The Story of -1. Princeton, NJ: Princeton University Press, 2007.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Complex Arithmetic." §5.4 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 171-172, 1992.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 21-23, 1986.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.
 الاكثر قراءة في التحليل العقدي
الاكثر قراءة في التحليل العقدي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















