Suppose that 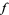 is an analytic function which is defined in the upper half-disk 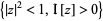. Further suppose that  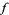extends to a continuous function on the real axis, and takes on real values on the real axis. Then  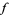can be extended to an analytic function on the whole disk by the formula

and the values for 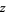 reflected across the real axis are the reflections of  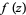across the real axis. It is easy to check that the above function is complex differentiable in the interior of the lower half-disk. What is remarkable is that the resulting function must be analytic along the real axis as well, despite no assumptions of differentiability.

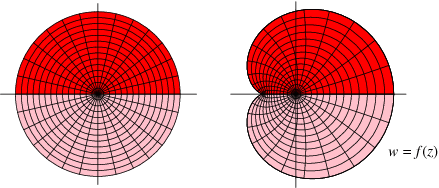
This is called the Schwarz reflection principle, and is sometimes also known as Schwarz's symmetric principle (Needham 2000, p. 257). The diagram above shows the reflection principle applied to a function 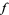 defined for the upper half-disk (left figure; red) and its image (right figure; red). The function is real on the real axis, so it is possible to extend the function to the reflected domain (left and right figures; pink).

For the reflected function to be continuous, it is necessary for the values at the boundary to be continuous and to fall on the line being reflected. The reflection principle also applies in the generality of reflecting along any line, not just the real axis, in which case the function 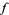 has to take values along a line in the range. In fact, any arc which has a neighborhood biholomorphic to a straight line can be reflected across. The basic example is the boundary of the unit circle which is mapped to the real axis by .

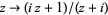The reflection principle can also be used to reflect a harmonic function which extends continuously to the zero function on its boundary. In this case, for negative 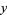, defining

extends 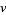 to a harmonic function on the reflected domain. Again note that it is necessary for 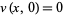. This result provides a way of extending a harmonic function from a given open set to a larger open set (Krantz 1999, p. 95).

REFERENCES:

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 195 and 213, 2003.

Krantz, S. G. Handbook of Complex Variables. Boston, MA: Birkhäuser, 1999.

Needham, T. Visual Complex Analysis. New York: Clarendon Press, 2000.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمَع العلمي يقيم مسابقة الكوثر الخاصة بترتيل القرآن الكريم في كربلاء

قسم الشؤون الفكرية والثقافية يُصدر العدد الثالث والعشرين من مجلّة (أوراق معرفية)

قسم التربية والتعليم يُطلق الموسم التدريبيّ الصيفيّ لملاكات مجموعة العميد التربوية

المجمَع العلمي يُطلق المرحلة الثالثة من مشروع أمير القرّاء الوطني

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد