
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2018
Date: 30-9-2019
Date: 9-8-2019
|
For a curve with radius vector 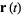 , the unit tangent vector
, the unit tangent vector 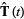 is defined by
is defined by
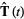 |
 |
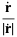 |
(1) |
 |
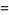 |
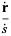 |
(2) |
 |
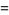 |
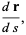 |
(3) |
where 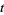 is a parameterization variable,
is a parameterization variable, 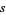 is the arc length, and an overdot denotes a derivative with respect to
is the arc length, and an overdot denotes a derivative with respect to 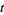 ,
, 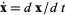 . For a function given parametrically by
. For a function given parametrically by 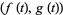 , the tangent vector relative to the point
, the tangent vector relative to the point 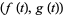 is therefore given by
is therefore given by
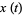 |
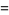 |
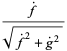 |
(4) |
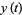 |
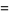 |
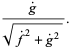 |
(5) |
To actually place the vector tangent to the curve, it must be displaced by 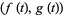 . It is also true that
. It is also true that
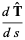 |
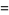 |
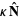 |
(6) |
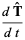 |
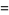 |
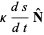 |
(7) |
![[T^.,T^..,T^...]](http://mathworld.wolfram.com/images/equations/TangentVector/Inline31.gif) |
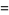 |
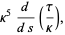 |
(8) |
where 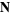 is the normal vector,
is the normal vector, 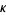 is the curvature,
is the curvature,  is the torsion, and
is the torsion, and ![[A,B,C]](http://mathworld.wolfram.com/images/equations/TangentVector/Inline37.gif) is the scalar triple product.
is the scalar triple product.
REFERENCES:
Gray, A. "Tangent and Normal Lines to Plane Curves." §5.5 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 108-111, 1997.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|