


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-3-2019
Date: 1-8-2019
Date: 24-3-2019
|
A theorem about (or providing an equivalent definition of) compact sets, originally due to Georg Cantor. Given a decreasing sequence of bounded nonempty closed sets
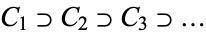 |
in the real numbers, then Cantor's intersection theorem states that there must exist a point 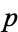 in their intersection,
in their intersection, 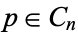 for all
for all 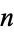 . For example,
. For example, ![0 in intersection [0,1/n]](http://mathworld.wolfram.com/images/equations/CantorsIntersectionTheorem/Inline4.gif) . It is also true in higher dimensions of Euclidean space.
. It is also true in higher dimensions of Euclidean space.
Note that the hypotheses stated above are crucial. The infinite intersection of open intervals may be empty, for instance 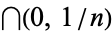 . Also, the infinite intersection of unbounded closed sets may be empty, e.g.,
. Also, the infinite intersection of unbounded closed sets may be empty, e.g., ![intersection [n,infty]](http://mathworld.wolfram.com/images/equations/CantorsIntersectionTheorem/Inline6.gif) .
.
Cantor's intersection theorem is closely related to the Heine-Borel theorem and Bolzano-Weierstrass theorem, each of which can be easily derived from either of the other two. It can be used to show that the Cantor set is nonempty.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|