


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-10-2019
Date: 20-8-2018
Date: 18-8-2019
|
Apéry's constant is defined by
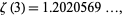 |
(1) |
(OEIS A002117) where 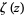 is the Riemann zeta function. Apéry (1979) proved that
is the Riemann zeta function. Apéry (1979) proved that 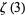 is irrational, although it is not known if it is transcendental. Sorokin (1994) and Nesterenko (1996) subsequently constructed independent proofs for the irrationality of
is irrational, although it is not known if it is transcendental. Sorokin (1994) and Nesterenko (1996) subsequently constructed independent proofs for the irrationality of 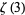 (Hata 2000).
(Hata 2000). 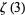 arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio, computed using quantum electrodynamics.
arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio, computed using quantum electrodynamics.
The following table summarizes progress in computing upper bounds on the irrationality measure for 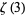 . Here, the exact values for
. Here, the exact values for 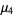 is given by
is given by
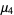 |
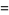 |
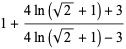 |
(2) |
 |
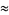 |
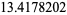 |
(3) |
(Hata 2000).
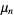 |
upper bound | reference |
| 1 | 5.513891 | Rhin and Viola (2001) |
| 2 | 8.830284 | Hata (1990) |
| 3 | 12.74359 | Dvornicich and Viola (1987) |
| 4 | 13.41782 | Apéry (1979), Sorokin (1994), Nesterenko (1996), Prévost (1996) |
Beukers (1979) reproduced Apéry's rational approximation to 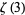 using the triple integral of the form
using the triple integral of the form
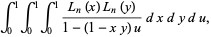 |
(4) |
where 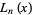 is a Legendre polynomial. Beukers's integral is given by
is a Legendre polynomial. Beukers's integral is given by
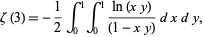 |
(5) |
a result that is a special case of what is known as Hadjicostas's formula.
This integral is closely related to 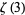 using the curious identity
using the curious identity
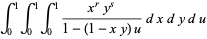 |
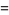 |
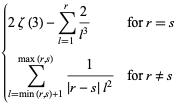 |
(6) |
 |
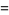 |
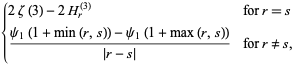 |
(7) |
where 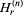 is a generalized harmonic number and
is a generalized harmonic number and 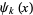 is a polygamma function (Hata 2000).
is a polygamma function (Hata 2000).
Sums related to 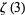 include
include
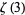 |
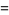 |
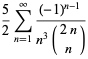 |
(8) |
 |
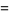 |
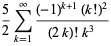 |
(9) |
(used by Apéry), the related sum
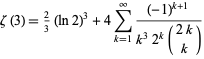 |
(10) |
as first proved by G. Huvent in 2002 (Gourevitch) and rediscovered by B. Cloitre (pers. comm., Oct. 8, 2004), and
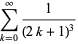 |
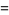 |
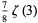 |
(11) |
 |
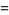 |
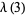 |
(12) |
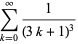 |
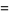 |
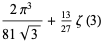 |
(13) |
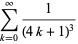 |
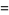 |
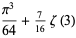 |
(14) |
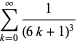 |
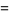 |
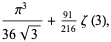 |
(15) |
where 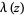 is the Dirichlet lambda function. The above equations are special cases of a general result due to Ramanujan (Berndt 1985).
is the Dirichlet lambda function. The above equations are special cases of a general result due to Ramanujan (Berndt 1985).
Apéry's constant is given by an infinite family BBP-type formulas of the form
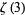 |
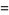 |
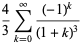 |
(16) |
 |
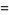 |
![4/3sum_(k=0)^(infty)(-1)^k[1/((3k+1)^3)-1/((3k+2)^3)+1/((3k+3)^3)]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline53.gif) |
(17) |
 |
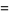 |
![3/2sum_(k=0)^(infty)(-1)^k[1/((3k+1)^3)-1/((3k+2)^3)-2/((3k+3)^3)]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline56.gif) |
(18) |
 |
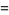 |
![4/3sum_(k=0)^(infty)(-1)^k[1/((5k+1)^3)-1/((5k+2)^3)+1/((5k+3)^3)-1/((5k+4)^3)+1/((5k+5)^3)]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline59.gif) |
(19) |
 |
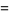 |
![1/(15)sum_(k=0)^(infty)(-1)^k[(21)/((5k+1)^3)-(21)/((5k+2)^3)+(21)/((5k+3)^3)-(21)/((5k+4)^3)-(104)/((5k+5)^3)]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline62.gif) |
(20) |
 |
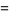 |
![4/3sum_(k=0)^(infty)(-1)^k[1/((7k+1)^3)-1/((7k+2)^3)+1/((7k+3)^3)-1/((7k+4)^3)+1/((7k+5)^3)-1/((7k+6)^3)+1/((7k+7)^3)]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline65.gif) |
(21) |
 |
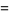 |
![1/(30)sum_(k=0)^(infty)(-1)^k[(41)/((7k+1)^3)-(41)/((7k+2)^3)+(41)/((7k+3)^3)-(41)/((7k+4)^3)+(41)/((7k+5)^3)-(41)/((7k+6)^3)+(302)/((7k+7)^3)]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline68.gif) |
(22) |
(E. W. Weisstein, Feb. 25, 2006), and the amazing two special sums
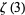 |
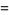 |
![1/(672)sum_(k=0)^(infty)1/(4096^k)[(2048)/((24k+1)^3)-(11264)/((24k+2)^3)-(1024)/((24k+3)^3)+(11776)/((24k+4)^3)-(512)/((24k+5)^3)+(4096)/((24k+6)^3)+(256)/((24k+7)^3)+(3456)/((24k+8)^3)+(128)/((24k+9)^3)-(704)/((24k+10)^3)-(64)/((24k+11)^3)-(128)/((24k+12)^3)-(32)/((24k+13)^3)-(176)/((24k+14)^3)+(16)/((24k+15)^3)+(216)/((24k+16)^3)+8/((24k+17)^3)+(64)/((24k+18)^3)-4/((24k+19)^3)+(46)/((24k+20)^3)-2/((24k+21)^3)-(11)/((24k+22)^3)+1/((24k+23)^3)]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline71.gif) |
(23) |
 |
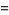 |
![9/(224)sum_(k=0)^(infty)1/(4096^k)[(1024)/((24k+2)^3)-(3072)/((24k+3)^3)+(512)/((24k+4)^3)+(1024)/((24k+6)^3)+(1152)/((24k+8)^3)+(384)/((24k+9)^3)+(64)/((24k+10)^3)+(128)/((24k+12)^3)+(16)/((24k+14)^3)+(48)/((24k+15)^3)+(72)/((24k+16)^3)+(16)/((24k+18)^3)+2/((24k+20)^3)-6/((24k+21)^3)+1/((24k+22)^3)].](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline74.gif) |
(24) |
Determining a sum of this type is given as an exercise by Bailey et al. (2007, p. 225; typo corrected).
A beautiful double series for 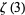 is given by
is given by
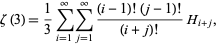 |
(25) |
where 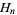 is a harmonic number (O. Oloa, pers. comm., Dec. 30, 2005).
is a harmonic number (O. Oloa, pers. comm., Dec. 30, 2005).
Apéry's proof relied on showing that the sum
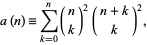 |
(26) |
where 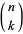 is a binomial coefficient, satisfies the recurrence relation
is a binomial coefficient, satisfies the recurrence relation
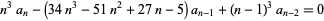 |
(27) |
(van der Poorten 1979, Zeilberger 1991). The characteristic polynomial 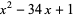 has roots
has roots 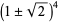 , so
, so
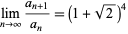 |
(28) |
is irrational and 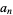 cannot satisfy a two-term recurrence (Jin and Dickinson 2000).
cannot satisfy a two-term recurrence (Jin and Dickinson 2000).
Apéry's constant is also given by
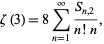 |
(29) |
where 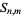 is a Stirling number of the first kind. This can be rewritten as
is a Stirling number of the first kind. This can be rewritten as
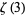 |
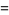 |
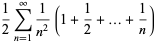 |
(30) |
 |
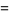 |
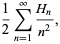 |
(31) |
where 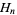 is the
is the 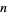 th harmonic number (Castellanos 1988).
th harmonic number (Castellanos 1988).
Integrals for 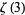 include
include
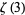 |
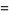 |
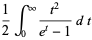 |
(32) |
 |
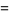 |
![8/7[1/4pi^2ln2+2int_0^(pi/2)xln(sinx)dx].](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline96.gif) |
(33) |
Gosper (1990) gave
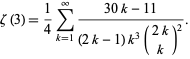 |
(34) |
A continued fraction involving Apéry's constant is
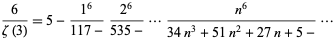 |
(35) |
(Apéry 1979, Le Lionnais 1983). Amdeberhan (1996) used Wilf-Zeilberger pairs 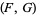 with
with
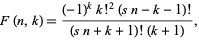 |
(36) |
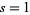 to obtain
to obtain
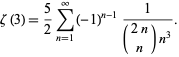 |
(37) |
For 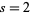 ,
,
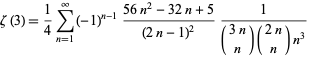 |
(38) |
(Boros and Moll 2004, p. 236; Amdeberhan 1996), and for 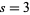 ,
,
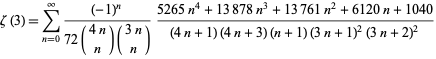 |
(39) |
(Amdeberhan 1996). The corresponding 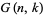 for
for 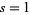 and 2 are
and 2 are
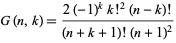 |
(40) |
and
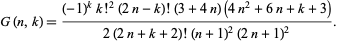 |
(41) |
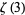 is related to the Glaisher-Kinkelin constant
is related to the Glaisher-Kinkelin constant 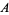 and polygamma function
and polygamma function 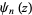 by
by
![zeta(3)=2/3pi^2[12psi_(-4)(1)-6lnA-ln(2pi)].](http://mathworld.wolfram.com/images/equations/AperysConstant/NumberedEquation18.gif) |
(42) |
Gosper (1996) expressed 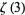 as the matrix product
as the matrix product
![lim_(N->infty)product_(n=1)^NM_n=[0 zeta(3); 0 1],](http://mathworld.wolfram.com/images/equations/AperysConstant/NumberedEquation19.gif) |
(43) |
where
![M_n=[((n+1)^4)/(4096(n+5/4)^2(n+7/4)^2) (24570n^4+64161n^3+62152n^2+26427n+4154)/(31104(n+1/3)(n+1/2)(n+2/3)); 0 1]](http://mathworld.wolfram.com/images/equations/AperysConstant/NumberedEquation20.gif) |
(44) |
which gives 12 bits per term. The first few terms are
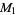 |
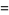 |
![[1/(19600) (2077)/(1728); 0 1]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline109.gif) |
(45) |
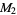 |
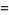 |
![[1/(9801) (7561)/(4320); 0 1]](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline112.gif) |
(46) |
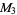 |
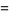 |
![[9/(67600) (50501)/(20160); 0 1],](http://mathworld.wolfram.com/images/equations/AperysConstant/Inline115.gif) |
(47) |
which gives
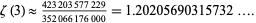 |
(48) |
Given three integers chosen at random, the probability that no common factor will divide them all is
![[zeta(3)]^(-1) approx 1.20206^(-1) approx 0.831907.](http://mathworld.wolfram.com/images/equations/AperysConstant/NumberedEquation22.gif) |
(49) |
B. Haible and T. Papanikolaou computed 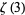 to
to 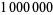 digits using a Wilf-Zeilberger pair identity with
digits using a Wilf-Zeilberger pair identity with
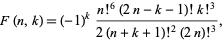 |
(50) |
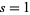 , and
, and 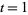 , giving the rapidly converging
, giving the rapidly converging
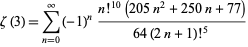 |
(51) |
(Amdeberhan and Zeilberger 1997). The record as of Dec. 1998 was 128 million digits, computed by S. Wedeniwski.
REFERENCES:
Amdeberhan, T. "Faster and Faster Convergent Series for 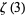 ." Electronic J. Combinatorics 3, No. 1, R13, 1-2, 1996. http://www.combinatorics.org/Volume_3/Abstracts/v3i1r13.html.
." Electronic J. Combinatorics 3, No. 1, R13, 1-2, 1996. http://www.combinatorics.org/Volume_3/Abstracts/v3i1r13.html.
Amdeberhan, T. and Zeilberger, D. "Hypergeometric Series Acceleration via the WZ Method." Electronic J. Combinatorics 4, No. 2, R3, 1-3, 1997. http://www.combinatorics.org/Volume_4/Abstracts/v4i2r3.html. Also available at http://www.math.temple.edu/~zeilberg/mamarim/mamarimhtml/accel.html.
Apéry, R. "Irrationalité de 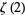 et
et 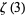 ." Astérisque 61, 11-13, 1979.
." Astérisque 61, 11-13, 1979.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.
Preprint dated Feb. 22, 2003 available at http://www.nersc.gov/~dhbailey/dhbpapers/bcnormal.pdf.
Berndt, B. C. Ramanujan's Notebooks: Part I. New York: Springer-Verlag, 1985.
Beukers, F. "A Note on the Irrationality of 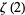 and
and 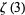 ." Bull. London Math. Soc. 11, 268-272, 1979.
." Bull. London Math. Soc. 11, 268-272, 1979.
Beukers, F. "Another Congruence for the Apéry Numbers." J. Number Th. 25, 201-210, 1987.
Boros, G. and Moll, V. Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, 2004.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. "The Great Enigma." In The Book of Numbers. New York: Springer-Verlag, pp. 261-262, 1996.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 76 and 371, 2004.
Dvornicich, R. and Viola, C. "Some Remarks on Beukers' Integrals." In Number Theory, Colloq. Math. Soc. János Bolyai, Vol. 51.Amsterdam, Netherlands: North-Holland, pp. 637-657, 1987.
Ewell, J. A. "A New Series Representation for 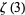 ." Amer. Math. Monthly 97, 219-220, 1990.
." Amer. Math. Monthly 97, 219-220, 1990.
Finch, S. R. "Apéry's Constant." §1.6 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 40-53, 2003.
Gosper, R. W. "Strip Mining in the Abandoned Orefields of Nineteenth Century Mathematics." In Computers in Mathematics (Ed. D. V. Chudnovsky and R. D. Jenks). New York: Dekker, 1990.
Gosper, R. W. "Zeta(3) to 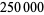 digits." math-fun@cs.arizona.edu posting, Sept. 1, 1996.
digits." math-fun@cs.arizona.edu posting, Sept. 1, 1996.
Gourevitch, P. "L'univers de 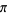 ." http://www.pi314.net/hypergse11.php.
." http://www.pi314.net/hypergse11.php.
Gutnik, L. A. "On the Irrationality of Some Quantities Containing 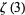 ." Acta Arith. 42, 255-264, 1983. English translation in Amer. Math. Soc. Transl. 140, 45-55, 1988.
." Acta Arith. 42, 255-264, 1983. English translation in Amer. Math. Soc. Transl. 140, 45-55, 1988.
Haible, B. and Papanikolaou, T. "Fast Multiprecision Evaluation of Series of Rational Numbers." Technical Report TI-97-7. Darmstadt, Germany: Darmstadt University of Technology, Apr. 1997.
Hata, M. "A New Irrationality Measure for 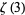 ." Acta Arith. 92, 47-57, 2000.
." Acta Arith. 92, 47-57, 2000.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 42, 2003.
Huvent, G. "Formules d'ordre supérieur." Pi314.net, 2002. http://s146372241.onlinehome.fr/web/pi314.net/hypergse11.php#x13-107002r480.
Huylebrouck, D. "Similarities in Irrationality Proofs for 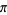 ,
, 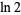 ,
, 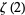 , and
, and 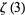 ." Amer. Math. Monthly 108, 222-231, 2001.
." Amer. Math. Monthly 108, 222-231, 2001.
Jin, Y. and Dickinson, H. "Apéry Sequences and Legendre Transforms." J. Austral. Math. Soc. Ser. A 68, 349-356, 2000.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 36, 1983.
Nesterenko, Yu. V. "A Few Remarks on 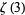 ." Mat. Zametki 59, 865-880, 1996. English translation in Math. Notes 59, 625-636, 1996.
." Mat. Zametki 59, 865-880, 1996. English translation in Math. Notes 59, 625-636, 1996.
Plouffe, S. "Table of Current Records for the Computation of Constants." http://pi.lacim.uqam.ca/eng/records_en.html.
Prévost, M. "A New Proof of the Irrationality of 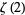 and
and 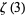 using Padé Approximants." J. Comput. Appl. Math. 67, 219-235, 1996.
using Padé Approximants." J. Comput. Appl. Math. 67, 219-235, 1996.
Rhin, G. and Viola, C. "The Group Structure for 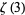 ." Acta Arith. 97, 269-293, 2001.
." Acta Arith. 97, 269-293, 2001.
Sloane, N. J. A. Sequence A002117/M0020 in "The On-Line Encyclopedia of Integer Sequences."
Sorokin, V. N. "Hermite-Padé Approximations for Nikishin Systems and the Irrationality of 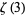 ." Uspekhi Mat. Nauk 49, 167-168, 1994. English translation in Russian Math. Surveys 49, 176-177, 1994.
." Uspekhi Mat. Nauk 49, 167-168, 1994. English translation in Russian Math. Surveys 49, 176-177, 1994.
Srivastava, H. M. "Some Simple Algorithms for the Evaluations and Representations of the Riemann Zeta Function at Positive Integer Arguments." J. Math. Anal. Appl. 246, 331-351, 2000.
van der Poorten, A. "A Proof that Euler Missed... Apéry's Proof of the Irrationality of 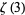 ." Math. Intel. 1, 196-203, 1979.
." Math. Intel. 1, 196-203, 1979.
Wedeniwski, S. "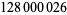 Digits of Zeta(3)." http://pi.lacim.uqam.ca/piDATA/Zeta3.txt.
Digits of Zeta(3)." http://pi.lacim.uqam.ca/piDATA/Zeta3.txt.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 33, 1986.
Zeilberger, D. "The Method of Creative Telescoping." J. Symb. Comput. 11, 195-204, 1991.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|