Laplace's Equation--Toroidal Coordinates

In toroidal coordinates, Laplace's equation becomes

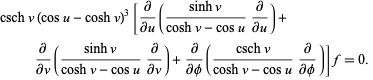(1)

Attempt separation of variables by plugging in the trial solution

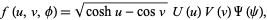(2)

then divide the result by 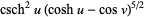 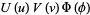 to obtain

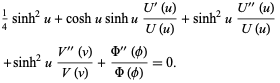(3)

The function 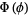 then separates with

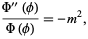(4)

giving solution

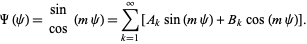(5)

Plugging 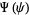 back in and dividing by  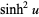gives

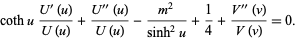(6)

The function 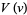 then separates with

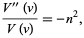(7)

giving solution

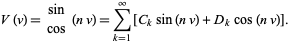(8)

Plugging 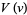 back in and multiplying by  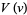gives

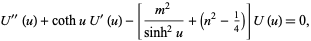(9)

which can also be written

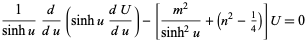(10)

(Arfken 1970, pp. 114-115). Laplace's equation is partially separable, although the Helmholtz differential equation is not.

Solutions to the differential equation for 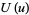 are known as toroidal functions.

REFERENCES:

Arfken, G. "Toroidal Coordinates 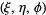." §2.13 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 112-115, 1970.

Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 264-266, 1959.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 666, 1953.