تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Integrating Factor
المؤلف:
Adams, R. A
المصدر:
_A Complete Course, 4th ed. Reading, MA_ Addison Wesley, 1999
الجزء والصفحة:
...
13-6-2018
1193
+
-
20
Integrating Factor
An integrating factor is a function by which an ordinary differential equation can be multiplied in order to make it integrable. For example, a linear first-order ordinary differential equation of type
 |
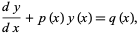(1) |
where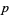 
and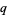 
are given continuous functions, can be made integrable by letting 
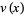be a function such that
 |
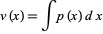(2) |
and
 |
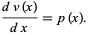(3) |
Then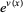 
would be the integrating factor such that multiplying by 
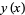gives the expression
![d/(dx)[e^(v(x))y(x)]](http://mathworld.wolfram.com/images/equations/IntegratingFactor/Inline6.gif) |
 |
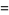![e^(v(x))[(dy(x))/(dx)+p(x)y(x)]](http://mathworld.wolfram.com/images/equations/IntegratingFactor/Inline8.gif) |
(4) |
 |
 |
 |
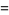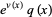(5) |
using the product rule. Integrating both sides with respect to 
then gives the solution
 |
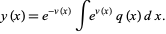(6) |
REFERENCES:
Adams, R. A. Calculus: A Complete Course, 4th ed. Reading, MA: Addison Wesley, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 526-529, 1953.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
مواضيع ذات صلة
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
