Weierstrass Function

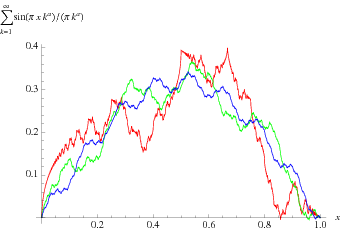
The pathological function

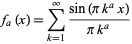(originally defined for 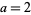) that is continuous but differentiable only on a set of points of measure zero. The plots above show  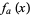for 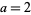 (red), 3 (green), and 4 (blue).

The function was published by Weierstrass but, according to lectures and writings by Kronecker and Weierstrass, Riemann seems to have claimed already in 1861 that the function 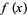 is not differentiable on a set dense in the reals. However, Ullrich (1997) indicates that there is insufficient evidence to decide whether Riemann actually bothered to give a detailed proof for this claim. du Bois-Reymond (1875) stated without proof that every interval of  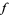contains points at which  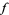does not have a finite derivative, and Hardy (1916) proved that it does not have a finite derivative at any irrational and some of the rational points. Gerver (1970) and Smith (1972) subsequently proved that  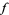has a finite derivative (namely, 1/2) at the set of points  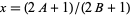where 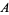and 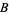 are integers. Gerver (1971) then proved that  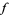is not differentiable at any point of the form  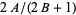or 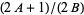. Together with the result of Hardy that  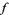is not differentiable at any irrational value, this completely solved the problem of the differentiability .

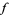Amazingly, the value of 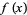 can be computed exactly for rational number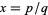s  as

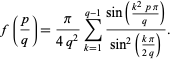REFERENCES:

Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.

Berry, M. V. and Lewis, Z. V. "On the Weierstrass-Mandelbrot Function." Proc. Roy. Soc. London Ser. A 370, 459-484, 1980.

Chamizo, F. and Córdoba, A. "Differentiability and Dimension of Some Fractal Fourier Series." Adv. Math. 142, 335-354, 1999.

Darboux, G. "Mémoire sur les fonctions discontinues." Ann. l'École Normale, Ser. 2 4, 57-112, 1875.

Darboux, G. "Mémoire sur les fonctions discontinues." Ann. l'École Normale, Ser. 2 8, 195-202, 1879.

du Bois-Reymond, P. "Versuch einer Klassification der willkürlichen Functionen reeller Argumente nach ihren Änderungen in den kleinsten Intervallen." J. für Math. 79, 21-37, 1875.

Duistermaat, J. J. "Self-Similarity of 'Riemann's Nondifferentiable Function.' " Nieuw Arch. Wisk. 9, 303-337, 1991.

Esrafilian, E. and Shidfar, A. "Hölder Continuity of Cellerier's Non-Differentiable Function." Punjab Univ. J. Math. (Lahore) 28, 118-121, 1995.

Faber, G. "Einfaches Beispiel einer stetigen nirgends differentiierbaren [sic] Funktion." Jahresber. Deutschen Math. Verein. 16, 538-540, 1907.

Falconer, K. Fractal Geometry: Mathematical Foundations and Applications. New York: Wiley, 1990.

Gerver, J. "The Differentiability of the Riemann Function at Certain Rational Multiples of 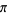." Amer. J. Math. 92, 33-55, 1970.

Gerver, J. "More on the Differentiability of the Riemann Function." Amer. J. Math. 93, 33-41, 1971.

Girgensohn, R. "Functional Equations and Nowhere Differentiable Functions." Aeq. Math. 46, 243-256, 1993.

Gluzman, S. and Sornette, D. "Log-Periodic Route to Fractal Functions." 4 Oct 2001. http://arxiv.org/abs/cond-mat/0106316.

Hairer, E. and Wanner, G. Analysis by Its History. New York: Springer-Verlag, 1996.

Hardy, G. H. "Weierstrass's Non-Differentiable Function." Trans. Amer. Math. Soc. 17, 301-325, 1916.

Havil, J. "Weierstrass Function." §D.2, Appendix D, in Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 230-231, 2003.

Hu, T. Y. and Lau, K.-S. "Fractal Dimensions and Singularities of the Weierstrass Type Functions." Trans. Amer. Math. Soc. 335, 649-665, 1993.

Hunt, B. R. "The Hausdorff Dimension of Graphs of Weierstrass Functions." Proc. Amer. Math. Soc. 126, 791-800, 1998.

Jaffard, S. "The Spectrum of Singularities of Riemann's Function." Rev. Mat. Iberoamericana 12, 441-460, 1996.

Kairies, H.-H. "Functional Equations for Peculiar Functions." Aeq. Math. 53, 207-241, 1997.

Kawamoto, S. and Tsubata, T. "The Weierstrass Function of Chaos Map with Exact Solution." J. Phys. Soc. Japan 66, 2209-2210, 1997.

Kritikos, H. N. and Jaggard, D. L. (Eds.). Recent Advances in Electromagnetic Theory. New York: Springer-Verlag, 1992.

Landsberg, G. "Über Differentziierbarkeit stetiger Funktionen." Jahresber. Deutschen Math. Verein. 17, 46-51, 1908.

Lerch, M. "Ueber die Nichtdifferentiirbarkeit [sic] gewisser Functionen." J. reine angew. Math. 13, 126-138, 1888.

Mandelbrot, B. B. "Weierstrass Functions and Kin. Ultraviolet and Infrared Catastrophe." The Fractal Geometry of Nature. New York: W. H. Freeman, pp. 388-390, 1983.

Metzler, W. "Note on a Chaotic Map That Generates Nowhere-Differentiability." Math. Semesterber. 40, 87-90, 1993.

Pickover, C. A. Keys to Infinity. New York: Wiley, p. 190, 1995.

Salzer, H. E. and Levine, N. "Table of a Weierstrass Continuous Non-Differentiable Function." Math. Comput. 15, 120-130, 1961.

Singh, A. N. The Theory and Construction of Non-Differentiable Functions. Lucknow: Newul Kishore Press, 1935.

Smith, A. "The Differentiability of Riemann's Functions." Proc. Amer. Math. Soc. 34, 463-468, 1972.

Sun, D. C. and Wen, Z. Y. "Dimension de Hausdorff des graphes de séries trigonométriques lacunaires." C. R. Acad. Sci. Paris Sér. I Math. 310, 135-140, 1990.

Sun, D. and Wen, Z. "The Hausdorff Dimension of Graph of a Class of Weierstrass Functions." Progr. Natur. Sci. (English Ed.) 6, 547-553, 1996.

Sun, D. C. and Wen, Z. Y. "The Hausdorff Dimension of a Class of Lacunary Trigonometric Series." In Harmonic Analysis: Proceedings of the Special Program held in Tianjin, March 1-June 30, 1988 (Ed. M.-T. Cheng, X. W. Zhou, and D. G. Deng). Berlin: Springer-Verlag, pp. 176-181, 1991.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 36, 2004. http://www.mathematicaguidebooks.org/.

Ullrich, P. "Anmerkungen zum 'Riemannschen Beispiel' 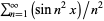 einer stetigen, nicht differenzierbaren Funktion." Results Math. 31, 245-265, 1997.

Volkert, K. "Die Geschichte der pathologischen Funktionen--Ein Beitrag zur Entstehung der mathematischen Methodologie." Arch. Hist. Exact Sci. 37, 193-232, 1987.

Weierstrass, K. Abhandlungen aus der Functionenlehre. Berlin: J. Springer, p. 97, 1886.