Continuity-Piecewise Function

A piecewise function is a function that is defined on a sequence of intervals. A common example is the absolute value,

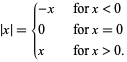(1)

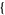Piecewise functions are implemented in the Wolfram Language as Piecewise[val1, cond1, val2, cond2, ...].

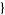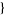Additional piecewise functions include the Heaviside step function, rectangle function, and triangle function.

Semicolons and commas are sometimes used at the end of either the left or the right column, with particular usage apparently depending on the author. The words "if" and "for" are sometimes used in the right column, as is "otherwise" for the final (default) case.

For example, Knuth (1996, pp. 175 and 180) uses the notations

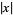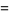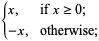			(2)
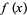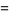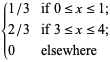			(3)
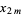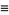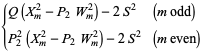			(4)

both with and without the left-column commas. Similarly, Arfken (1985, pp. 488-489) uses

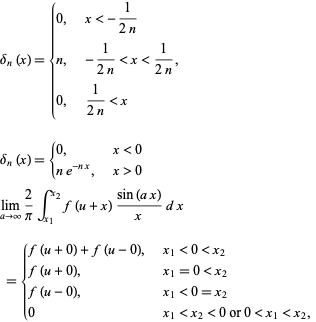(5)

which lacks semicolons but only sometimes lacks right-column commas.

In this work, commas and semicolons are not used.

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.

Knuth, D. E. The TEXBook. Boston, MA: Addison-Wesley, 1996.

 Rytin, M. "Integration of Piecewise Functions with Applications." http://library/infocenter/MathSource/5117.