Spiral Orbit
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 10
1-8-2016
1347
Spiral Orbit
A particle moves in two dimensions under the influence of a central force determined by the potential V(r) = αrp + βrq Find the powers p and q which make it possible to achieve a spiral orbit of the form r = cθ2 with a constant.
SOLUTION
The solution may be obtained most quickly by employing the differential equation for the orbit, whereby the time dependence is eliminated from the equation of motion. The derivation proceeds from the definition of angular momentum which is conserved in central force motion, and consists of the substitution of (l/mr2) (d/dθ) for d/dt. In its final form, the equation reads as follows:
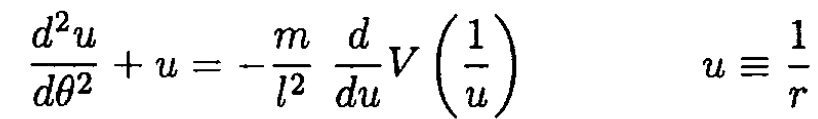(1)
We now substitute the proposed potential and orbit equation into (1):
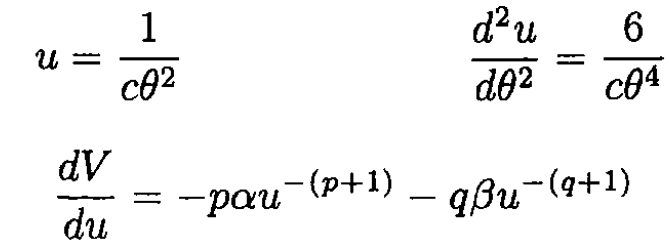
yielding
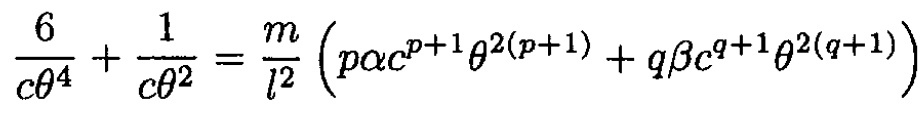(2)
Identifying powers of on the two sides of (2) gives
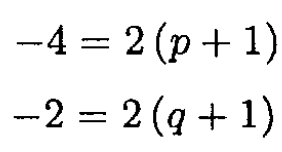
and therefore
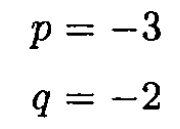
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
