الكون الأنيق لـ برايان غرين

ص334

تاسعاً : الثنائية في نظرية الأوتار

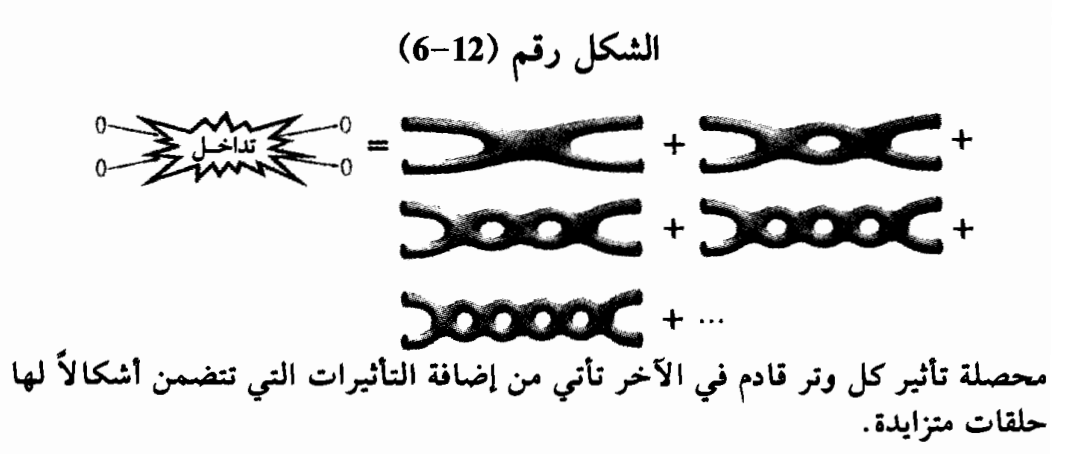
بتتبع خطوات ويتن لنبدأ بإحدى نظريات الأوتار الخمس، ولتكن نوع الأوتار 1، ونتخيل أن كل الأبعاد الفضائية التسعة مسطحة وغير ملفوفة. وهذا أمر غير واقعي بالطبع، لكنه يجعل النقاش أبسط ؛ وسنعود حالاً إلى الأبعاد المتجعدة. ولنبدأ بافتراض أن ثابت ازدواج الوتر أقل كثيراً من .1. وفي هذه الحالة فإن أدوات الاضطراب صالحة وبالتالي فإن العديد من تفاصيل خواص النظرية يمكن التوصل إليها بدقة، وقد تم ذلك بالفعل. فإذا زدنا من قيمة ثابت الازدواج لكنه ما زال أقل من 1 بشكل معقول، فإن الطرق الاضطرابية ستظل صالحة، لكن الخواص التفصيلية للنظرية ستتغير بعض الشيء - فمثلاً تتغير القيم العددية المصاحبة لتشتت وتر مبتعد عن الآخر بعض الشيء لأن العمليات التي تجري للحلقات المتعددة في الشكل رقم (12-6) تسهم بشكل أكبر عندما يزداد ثابت الازدواج. وفي ما عدا هذه التغييرات في تفاصيل الخواص العددية فإن المحتوى الفيزيائي الكلي يظل هو نفسه ما دام ثابت الازدواج يقع في حدود تطبيق الاضطراب.

فإذا زدنا من قيمة ثابت ازدواج الوتر من النوع 1 ليتخطى قيمة 1، ستصبح الطرق الاضطرابية غير صالحة وبذا فإننا سنركز فقط على المجموعة المحددة من الكتل والشحنات اللا اضطرابية - حالات BPS التي ما زال في مقدورنا إدراكها. وسنذكر هنا ما قاله ويتين وتأكد بعد ذلك من خلال بحوث مشتركة مع جو بولتشينسكي من جامعة كاليفورنيا - سانت باربارا تتفق هذه الخواص الازدواجية القوية لنظرية الأوتار من النوع 1 تماماً مع الخواص المعروفة لنظرية الأوتار هيتيروتيك عندما يكون للأخيرة قيمة صغيرة لثابت ازدواج الوتر الخاص بها. أي أنه عندما يكون ثابت الازدواج لأوتار النوع 1 كبيراً، فإن الكتل والشحنات المعنية والتي نعرف كيف نستخلصها تساوي بالضبط تلك الخاصة بأوتار هيتيروتيك- عندما يكون ثابت ازدواجه صغيرة. ويعطي ذلك إشارة قوية على أن هاتين النظريتين واللتان لأول وهلة مثل الماء السائل والثلج - تبدوان مختلفتين تماماً، هما في الواقع ثنائي. ويقترح ذلك - بقوة – أن فيزياء النظرية من النوع ] في حالة قيم ثابت الازدواج الخاص بها مماثلة تماماً لفيزياء نظرية هيتيروتيك عندما تكون قيم ثابت ازدواجها صغيرةً. وتقدم المجادلات المشابهة أدلة مقنعة بنفس الدرجة على أن العكس صحيح فيزياء النظرية من النوع 1 في حالة القيم الصغيرة لثابت ازدواجها مماثلة لفيزياء نظرية هيتيروتيك-O عندما يكون ثابت ازدواجها كبيراً. ومع أن النظريتين تبدوان وكأنهما غير مرتبطتين عند تحليلهما باستخدام منطلق التقريب الاضطرابي، فإننا نرى الآن أن كل واحدة منهما تتحول إلى الأخرى - الأمر الذي يشبه بعض الشيء التحول بين الماء السائل والثلج - عندما تتغير قيمة ثابت ازدواجهما.

ويعرف هذا النوع الجديد من النتائج المحورية والذي فيه فيزياء الازدواج القوي لإحدى النظريات يمكن التعبير عنه بفيزياء الازدواج الضعيف لنظرية أخرى باسم "ثنائية قوي-ضعيف" (Strong-Weak Duality). وكما في الثنائيات الأخرى التي ناقشناها سابقاً، فإن ذلك يدلنا على أن النظريتين المعنيتين ليستا في الواقع متمايزتين. وبالأحرى، فإنهما تقدمان توصيفاً مختلفاً لنفس أساس النظرية. وعلى عكس ثنائية اللغتين الإنكليزية - الصينية العادية، فإن ثنائية قوي - ضعيف" ذات مقدرة عظيمة. وعندما يكون ثابت الازدواج لأحد أعضاء ثنائي النظرية صغيراً فإننا نستطيع تحديد خواصها الفيزيائية مستخدمين الأدوات الاضطرابية المتطورة. أما إذا كان ثابت الازدواج للنظرية كبيراً وبالتالي لا تنجح الطرق الاضطرابية، فإننا يمكن أن نستخدم التوصيف الثنائي – التوصيف الذي يكون فيه ثابت الازدواج المقابل صغيراً - ونعود لتطبيق أدوات الاضطراب. وقد نتج من هذا التحول أن حصلنا على طرق كمية لتحليل نظرية كنا نعتقد في البداية أنها خارج  حدود إمكانياتنا النظرية.

وفي الواقع فإن البرهنة على أن فيزياء الازدواج القوي لنظرية الأوتار . النوع ] تناظر فيزياء الازدواج الضعيف لنظرية هيتيروتيك-O، والعكس، عمل في غاية الصعوبة لم يتوصل إليه أحد بعد. والسبب في ذلك بسيط. فأحد أعضاء زوج ثنائي النظريات المفترض لا يخضع للتحليلات الاضطرابية حيث أن ثابت الازدواج الخاص بها أكبر من اللازم. ويمنع ذلك الحسابات المباشرة للكثير من خواصها الفيزيائية وفي الحقيقة، إنها هذه النقطة بالضبط التي تجعل الثنائية

المفترضة ذات مقدرة عالية، لأنه إذا كانت صحيحة فإنها تقدم أداة جديدة لتحليل النظرية ذات الازدواج :القوي تطبيق الطرق الاضطرابية على توصيف ثنائي الازدواج الضعيف.

وحتى إذا لم نستطع أن نبرهن على أن النظريتين تكونان ثنائياً، فإن التوازن التام بين خواصهما الذي يمكن استخلاصه بكل ثقة يقدم دلائل مقنعة للغاية على أن علاقة ترابط ازدواج قوي ضعيف بين النظرية من النوع 1 ونظرية هيتيروتيك-O صحيحة. وفي الحقيقة جاءت كل الحسابات الذكية التي أجريت لاختبار الثنائية المقترحة بنتائج إيجابية. وقد اقتنع معظم منظري نظرية الأوتار بأن الثنائية أمر صحيح.

وباتباع نفس المنطق يمكن للمرء أن يدرس خواص الازدواج القوي لنظرية أوتار أخرى، ولتكن من نوع أوتار .IIB وكما ارتبط الأمر أصلاً بكل من هول و تاونسند وأيدته أبحاث عدد من الفيزيائيين اتضح أن هناك شيء ما بنفس الأهمية قد حدث. كلما زاد ثابت الازدواج لنوع أوتار IIB أكثر وأكثر فإن الخواص الفيزيائية التي ما زلنا قادرين على فهمها تبدو أنها تتوافق تماماً مع خواص الازدواج الضعيف للوتر من نوع IIB نفسه. وبمعنى آخر، فإن الوتر من نوع IIB يكون ثنائياً ذاتياً مع نفسه Self-Dual) وبالتحديد فإن التحاليل التفصيلية تقترح بإغراء انه إذا كان ثابت ازدواج النوع IIB أكبر من 1، وإذا كان علينا أن نغير من قيمته إلى معكوسه (وبذلك ستصبح قيمته أقل من 1)، فإن النظرية الناتجة ستكون بالتأكيد مماثلة تماماً لتلك التي بدأنا بها. ويشبه الأمر هنا ما وجدناه عندما حاولنا اعتصار بعد دائري على طول أقل من طول بلانك، فإننا إذا حاولنا زيادة قيمة ازدواج النوع IIB إلى قيمة أكبر من ،1، سيبين الثنائي الذاتي أن النظرية الناتجة مكافئة تماماً لنظرية النوع IIB ذات الازدواج الأقل من 1.

مواضيع ذات صلة

لصورة الشاملة ( تمهيد رياضي لنظرية-M)

هل يجيب أي مما سبق عن الأسئلة التي ما زالت بدون حل في نظرية الأوتار؟

الثقوب السوداء: منظور وتر/ نظرية - M

نظرية - M وشبكة الترابطات

السمة المفاجئة لنظرية -M: ديمقراطية متوسعة (نهاية احتكار الأوتار كبُنى أساسية)

بصيص من نظرية .M

الثنائية في نظرية الأوتار: من تعدد النظريات إلى وحدة الفيزياء

هل التقريب في الحدود المناسبة؟(ثابت ازدواج الوتر ومعضلة التقريب الاضطرابي)

موجز ما تم حتى الآن(الازدواجية في نظريات الأوتار)

نظرية الأوتار في فيزياء الكم: معادلات وتقنيات غير اضطرابية(معادلات نظرية الأوتار)

مقدرة التناظر (مقدرة التناظر والتناظر الفائق: مفاتيح فهم الازدواج القوي في نظريات الأوتار)

الجاذبية الفائقة (الجاذبية الفائقة والأبعاد الخفية: من الجسيمات النقطية إلى نظرية الأوتار)