يمكن أن تدور جسيمة أولية مثل الإلكترون حول نواة ذرية بنفس الطريقة تقريباً التي تدور بها الأرض حول الشمس. لكن في الوصف التقليدي للإلكترون كجسيمة نقطة، يبدو أنه لا تشابه هناك مع دوران الأرض حول محورها (في حركة مغزلية). وعندما يدور جسم حول نفسه (في حركة مغزلية) فإن النقاط الموجودة على محور الدوران – كما هو الحال في نقطة المركز في طبق فريسبي الدوار (Frisbee) - لا تتحرك. وإذا كان هناك أي شيء مثل النقطة بالفعل، فإنه لا يملك نقاطاً أخرى تقع خارج محور الدوران المعني. وبذلك قد يبدو أنه لا يوجد مفهوم لدوران مغزلي لجسم على شكل نقطة. ومنذ سنوات كثيرة مضت، فإن مثل هذا المنطق سقط ضحية لمفاجأة أخرى من ميكانيكا الكم.

وفي العام 1925، تحقق عالما الفضاء الهولنديان جورج أولينبيك وصمويل غودسميث من أن كثيراً من البيانات المحيرة والمتعلقة بخواص الضوء المنبعث والممتص بواسطة الذرات، يمكن تفسيرها إذا افترضنا أن للإلكترونات خواص مغناطيسية من نوع خاص جداً وقد بين العالم الفرنسي أندريه – ماري أمبير منذ بضع مئات من السنين، أن المغناطيسية تنتج من حركة الشحنة الكهربية. وقد تتبع أولينبيك وغودسميث هذا الخط واكتشفا أن هناك نوعاً معيناً واحداً فقط من حركة الإلكترون هو الذي يمكن أن يعطي الخواص المغناطيسية التي جاءت بها البيانات الحركة الدورانية - أي الحركة المغزلية وهكذا، على النقيض من التوقعات التقليدية، أعلن كل من أولينبيك وغودسميث أن الإلكترونات تشبه الأرض إلى حد ما في كونها تدور حول النواة وتدور حول نفسها (في حركة مغزلية).

هل كان أولينبيك وغودسميث يعنيان حرفياً أن الإلكترون يدور في حركة مغزلية؟ نعم ولا، والأمر الذي بينته أبحاثهما بالفعل هو أن هناك مفهوماً من ميكانيكا الكم حول الحركة المغزلية التي تشبه إلى حد ما الصورة العادية. لكن لها طبيعة كمية من ميكانيكا الكم). إنها واحدة من تلك الخواص الخاصة المجهري والتي تعيد صقل الأفكار الكلاسيكية لكنها تدخل مفهوم الكم المحقق تجريبياً فمثلاً تخيل لاعبة تزلج على الجليد وهي تدور في حركة مغزلية. فإذا ضمت ذراعيها إلى الداخل تزداد سرعة دورانها حول نفسها بينما إذا مدت ذراعيها إلى الخارج فإن دورانها حول نفسها يتباطأ. وآجلاً أو عاجلاً ستبطئ الحركة وتتوقف في النهاية اعتماداً على السرعة التي كانت تدور بها ويختلف هذا الأمر عن نوع الحركة المغزلية التي تناولها أولينبيك وغودسميث وتبعاً لأبحاثهما وللدراسات التي تبعت ذلك، فإن كل إلكترون في الكون يتحرك حركة مغزلية دائماً وأبداً بمعدل واحد ثابت لا يتغير أبداً. وحركة الإلكترون المغزلية ليست حالة حركة عابرة مثل كثير من الأشياء المألوفة والتي قد تدور في حركة مغزلية لسبب أو لآخر. وبدلاً من ذلك فإن دوران الإلكترون حول نفسه هو خاصية ذاتية تشبه كثيراً كتلته أو شحنته الكهربية. فإذا لم يقم الإلكترون بالدوران في حركة مغزلية، فإنه لن يصبح إلكتروناً.

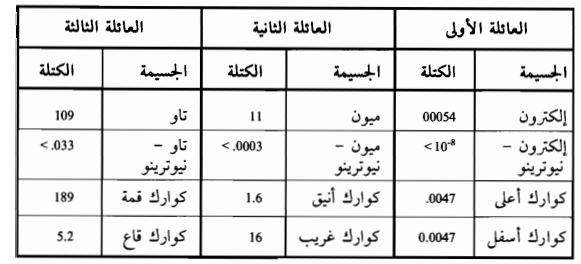
وبالرغم من أن الأبحاث المبكرة قد تركزت على الإلكترون، إلا أن الفيزيائيين قد بينوا في ما بعد أن هذه الأفكار عن الحركة المغزلية تنطبق بنفس الشكل على كل جسيمات المادة الموجودة ضمن العائلات الثلاث في الجدول رقم (1-1). وهذا الأمر صحيح حتى أدق التفاصيل: فكل جسيمات المادة ورفاقها من جسيمات المادة المضادة كذلك لها حركة مغزلية مساوية لحركة الإلكترون المغزلية. ففي لغة التخصص، يقول الفيزيائيون إن جسيمات المادة كلها لها سبين Spin - حركة مغزلية "سبين – 2/1 " ، حيث قيمة 2/1 تشير بصفة عامة لأحد مقاييس ميكانيكا الكم عن مدى سرعة دوران الإلكترون حول نفسه وفوق ذلك، بيَّن الفيزيائيون أن ناقلات القوى اللاجاذبية - الفوتونات والبوزونات الضعيفة القياسية والغليونات - لها أيضاً خاصية مغزلية ذاتية، اتضح أنها "ضعف" تلك التي لجسيمات المادة وكلها تملك "سبين - 1".

وماذا عن الجاذبية؟ تمكن الفيزيائيون حتى من قبل ظهور نظرية الأوتار، من تعيين قيمة "سبين" التي يجب على الغرافيتون المفترض أن يمتلكها لكي يكون ناقلاً لقوى الجاذبية والإجابة هي: ضعف قيمة الحركة المغزلية "سبين"

للفوتونات والبوزونات القياسية الضعيفة والغليونات – أي "سبين - 2". وفي مضمون نظرية الأوتار تكون الحركة المغزلية "سبين" - مثل الكتلة وشحنات القوى - تصاحب نسق الاهتزاز الذي يحدثه الوتر. وكما في حالة الجسيمات النقاط فإن الأمر هنا خادع بعض الشيء أن نظن أن الحركة المغزلية للوتر ناتجة من دورانه حول نفسه في المكان في حركة مغزلية، لكن هذه الصورة تعطي انطباعاً غير دقيق في الذهن وبهذه المناسبة، يمكن الآن أن نوضح أمراً هاماً كنا قد قابلناه من قبل في العام 1974 عندما أعلن تشيرك وشوارتز أنه يجب اعتبار نظرية الأوتار نظرية كم متضمنة لقوى الجاذبية، فقد أعلنا ذلك لأنهما وجدا أن للأوتار " بالضرورة نسقاً اهتزازياً في رصيدها، وهو لا كتلة له وله قيمة سبين السمات المميزة للغرافيتون وحيث يوجد الغرافيتون توجد الجاذبية. وبهذه الخلفية عن مفهوم الحركة المغزلية "سبين" من الممكن الآن أن نتحول إلى الدور الذي تلعبه في الكشف عن الثغرات الموجودة في نتائج كولمان - مانديولا المتعلقة بالتناظرات المحتملة في الطبيعة والتي سبق ذكرها في الجزء السابق.

الجدول(1-1)

مواضيع ذات صلة

كيف تبدو الأبعاد المتجعدة؟

المستتبعات الفيزيائية للأبعاد الإضافية

ألغاز الأبعاد الخفية: لماذا نعيش في ثلاثة أبعاد فقط؟"( بعض التساؤلات)

أبعاد أكثر ونظرية الأوتار

نظرية كالوزا - كلاين الحديثة

التوحد في الأبعاد الأعلى

الحركة جيئة وذهاباً على خرطوم المياه: تصور الأبعاد الخفية في الكون الأنيق

وهم المألوف: من أبعاد نيوتن إلى كون كالوزا متعدد الأبعاد

فكرة كالوزا وتنقيح كلاين

إحراج فائق ناجم عن الوفرة

حالة التناظر الفائق: ما قبل نظرية الأوتار

الكون في أصغر أبعاده ما الذي نعرفه عن المادة؟