
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
مبرهنة بيل وضرورة اللامحلية
المؤلف:
ديفيد والاس
المصدر:
فلسفة علم الفيزياء
الجزء والصفحة:
ص 106 – ص 110
2024-09-01
1265
تحظى الألعاب التعاونية – التي يتعاون فيها اللاعبون لتحقيق هدف مشترك – برواج كبير في هذه الأيام. وصحيح أنَّ «لعبة بيل»، وهي لعبة تعاونية يمارسها لاعبان، لا تستطيع أن تنافس الألعاب الأكثر إمتاعًا، لكن أهميتها الفلسفية تعوض ما تفتقر إليه في عنصر التسلية لممارسة هذه اللعبة، نحتاج إلى عملتين معدنيتين وبطاقتين وغرفتين؛ إذ يحصل كلُّ لاعب على واحدة من كل زوج قد تستقر العملتان على «الصورة» أو «الكتابة» عند رميهما؛ وللبطاقتين وجه أبيض وآخرُ أسود؛ ويجب أن تكون كلٌّ من الغرفتين بعيدةً عن الأخرى ومقفلة.
سأوضح الآن كيف يمكننا أن نلعب أنا وأنت جولة من اللعبة. ندخل الغرفتين ويقلب كلٌّ منَّا عملته المعدنية. بعد ذلك نضع البطاقتين بحيث إما أن يكون الوجه الأبيض إلى الأعلى أو الأسود. والحق أنَّ شروط الفوز غريبة بعض الشيء: فنحن نفوز إذا وضع كلانا البطاقتين على الوجه نفسه (كلتا البطاقتين على الوجه الأبيض أو كلتاهما على الوجه الأسود)؛ «إلا» إذا استقرت العملتان على «الكتابة» حين نقلبهما ، فحينها نفوز إذا اختلف الوجه العلوي للبطاقتين (أسود / أبيض أو أبيض / أسود). نلعب عدة جولات، وفي النهاية نحسب النقاط: النقاط هي المرات التي فزنا فيها. وفيما يلي ملخص القواعد:
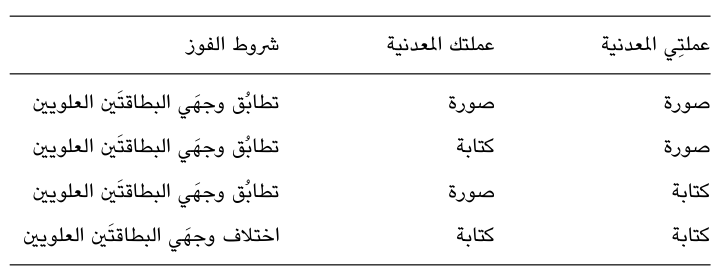
قبل بدء اللعب، يمكننا مقارنة الملاحظات كي يمكننا التوصل إلى أفضل استراتيجية ممكنة. فمن الاستراتيجيات الوجيهة على سبيل المثال، أن نتَّفق على وضع البطاقتين دومًا بحيث يكون الوجه الأبيض إلى أعلى مهما كانت الظروف. ووفقًا لتلك الاستراتيجية، سنفوز في ثلاثة أرباع المرات، ولن نخسر إلا إذا استقرت العملتان على وجه الكتابة.
ماذا إذا كنا نريد أداءً أفضل؛ أي إذا أردنا ألا نكتفي بالفوز في ثلاثة أرباع المرات بل في كل المرات؟ لن تجد صعوبة في إقناع نفسك باستحالة ذلك. لنفترض مثلًا أننا اتفقنا على أنك ستجعل وجه الورقة الأبيض هو الأعلى مهما حدث. سأحتاج أنا إلى وضع الوجه الأسود لأعلى إذا استقرت العملتان على وجه «الكتابة»، وأن أضع الوجه الأبيض لأعلى إذا كانت إحدى العملتين فقط هي التي استقرَّت على وجه «الكتابة»؛ لكنني كي أتمكن من ذلك، سأحتاج إلى رؤية عملتك مثلما سأحتاج إلى رؤية عملتي، وكلاهما في غرفة مختلفة. لا سبيل إذن إلى تجنُّب لعب البطاقة الخطأ في بعض الأحيان، وبهذا يؤدي احتمال واحد على الأقل من بين التوفيقات الأربعة المحتملة لقلب العملتين في الهواء إلى خسارتنا. ونحن نواجه مشكلات مماثلة أيا كانت الاستراتيجية التي نتَّبعها؛ إذ لا يستطيع كلانا سوى رؤية عملته؛ ولأن شروط الفوز تعتمد على خاصية مشتركة بين العملتين، فثمة نتيجة واحدة على الأقل من النتائج الأربع لقلب العملتين في الهواء ستؤدي إلى خسارتنا. ولهذا لا يمكننا الحصول على نتيجة أفضل من 75 بالمائة.
ماذا لو سمحنا بالعشوائية في الاستراتيجيات؟ يمكننا مثلًا أن نقرر مقدَّمًا اتباع استراتيجية مختلفة في كل جولة من اللعبة، يمكننا حتى أن نتخذ هذا القرار وفقًا لقلب العملة في الهواء أو دحرجة النرد. وهذا أيضًا لن يفيد ذلك أنه لا توجد استراتيجية من الاستراتيجيات «الخالصة» (غير العشوائية) تحقق نسبة نجاح أكبر من 75 بالمائة؛ ولهذا لا يزيد النجاح الذي يحققه مَنْج هذه الاستراتيجيات عشوائيا عن 75 بالمائة هو الآخر.
لكن لنفترض أننا توصلنا إلى لاعبين في هذه اللعبة تمكنا بالفعل من تحقيق نجاح يتجاوز 75 بالمائة. فكيف تأتّى لهما فعل ذلك؟ الاحتمالية الواضحة هي أنهما يغُشَّان؛ فربما أدخلا هاتفين محمولين أو ما شابه خلسةً إلى الغرفتين، وراحا يقارنان الملاحظات. يبدو إذن أننا أثبتنا أنه من دون الغش بتلك الطريقة، فأفضل درجة يمكن الحصول عليها في لعبة بيل هي 75 بالمائة؛ ومن ثم فإن تحقيق درجة تزيد على 75 بالمائة هو دليل على الغش.
نلفترض أننا نهتم «حقا» بمنع الغش. إليكم طريقة مؤكدة لتحقيق ذلك؛ وهي الحرص على أن تكون المسافة بين الغرفتين كبيرةً، بحيث لا يتمكن حتى الضوء من الانتقال من غرفة إلى أخرى في أثناء ممارسة اللعبة (ربما تكون الغرفة الأولى على الأرض، والغرفة الثانية في مدار حول كوكب المشتري، ولن نمارس اللعبة إلا لمدة عشر دقائق، أقل من المدة التي يستغرقها الضوء للسفر بين الكوكبين، وهي من 35 إلى 50 دقيقة). في هذه الحالة، يبدو الغش مستحيلا من الناحية الفيزيائية؛ إذ إنه سيتطلب إشارةً أسرع من الضوء.
يُطلَق على النتيجة المتمثلة في أن 75 بالمائة هي أقصى درجة ممكنة في لعبة بيل من دون وجود إشارة بين الغرفتين – اسم «متباينة بيل» نسبة إلى عالم الفيزياء جون بيل. إذا كسر حاجز هذه النتيجة، فسيعني ذلك، على ما أنه يبدو، توجد إشارة تسافر بين الغرفتين اللتين تُمارس فيهما اللعبة؛ وإذا كانت المسافة بين الغرفتين كبيرةً ولا يَسع الضوء أن يسافر بينهما، فلا بد أن تكون هذه الإشارة أسرع من الضوء.
في تجربة بارزة أُجريت في باريس عام 1986، أعد الان أسبكت جهازًا مارس لعبة بيل فعليًّا وفاز فيها بنسبة تزيد على 75 بالمائة من الوقت، لكنه لم يفز في كل المرات. (استخدم أسبكت أجهزة للتوزيع العشوائي بدلا من البشر، ويبدو نموذج المتباينة التفصيلي الذي أخلَّ به مختلفًا عن نموذج نسبة الـ 75 بالمائة الذي استخدمناه هنا، لكن الأفكار الأساسية لكليهما واحدة). ومنذ ذلك الوقت، تكرّرت نتيجة أسبكت مرةً بعد مرة. فلنتناول الآن تلك الطريقة وكيفية تنفيذها: نولّد أزواجًا من الجسيمات في الحالة الأحادية <SINGLET|، ونرسلها إلى الغرفتين وفي كل غرفة، قاسَ اللاعب (أو بالأحرى مجموعة الدوائر المؤتمتة التي تحلُّ محلَّ اللاعب) دوران الجسيم في أحد الاتجاهين المحتملين، مع تحديد اختيار الاتجاه عشوائيا عن طريق القرعة بالعملة المعدنية (عن طريق جهاز ميكانيكي يقوم بالتوزيع العشوائي في حقيقة الأمر). تُفسَّر نتيجة الدوران لأعلى على أنها وضع وجه البطاقة «الأبيض» لأعلى، بينما تُفسَّر نتيجة الدوران لأسفل على أنها وضع وجه البطاقة «الأسود» لأعلى. وعلى خلاف مناقشتنا السابقة للحالة الأحادية <|SINGLET، فليست اتجاهات القياس واحدة في حالة كل جسيم؛ لذلك لن نتنبأ بالارتباط المعاكس المثالي للنتائج: ما تتنبأ به نظرية الكم هو أن الارتباط المعاكس يصبح أضعف تدريجيًّا مع تباعد اتجاهات القياس.
صحيح أنَّ الرياضيات ذات الصلة تفوق مستوى هذا الكتاب، لكن سيكون من السهل وصفُ النتيجة النهائية؛ إذا نفَّذنا هذا البروتوكول: إعداد تسلسلات حالات الدوران وقياسها فستصبح انتيجة لعبة بيل حوالي 85 بالمائة؛ أي اعلى من الحد الذي تنص عليه متباينة بيل.
أول ما يمكننا استنتاجه من هذا هو أن التشابك الكمي اعقد من الترابط الاحتمالي.اذا استطعنا بشكل ما أن ننظر الى الحالة الاحادية |SINGLET> على انها تصف زوجا من حالات الدوران المحددة لكنها مرتبطة عكسيا، فان قياسات هذه الدورانات ستضم مزيجا عشوائيا (وبالغ التعقيد) من الاستراتيجيات، وقد رأينا انه ما من مزيج كهذا يمكن أن يتخطى حاجز 75 بالمائة. أيا يكن التشابك الكمي، فهو أغرب مما في تصورنا، ويبدو بالفعل أن اللامحلية سمة أصلية من سماته. ذلك ان الارتباطات بين قياسات الدوران عند قياس |SINGLET> أقوى كثيرا من أن تعزى ال أي وصف محلي أساسي.
غير أننا نستطيع ان نتعلم من التجارب التي تخل بمتباينة بيل ما هو اكثر من هذا بكثير. ذلك ان ما اشتققناه من المتباينة لم يستخدم ميكانيكا الكم في نهاية المطاف؛ وانما كان محض توضيح لان أي استراتيجية تكسر حاجز الـ 75 بالمائة في درجات لعبة بيل، لابد انها تستخدم نوعا من التفاعلات الأسرع من الضوء. وقد نجحت تجربة اسبكت وما تلاها من التجارب في تخطي حاز تلك الدرجة. اذن، حتى اث ثبت بطلان ميكانيكا الكم غدا، فان هذه التجربة تعد برهانا تجريبيا مباشرا على ان العالم ينطوي على عمليات تحدث بسرعة اكبر من سرعة الضوء، بل انها عمليات تحدث بسرعة اعتباطية وعلى نحو آني.
غير أن هذا الاستنتاج محل خلاف حاد. فمعظم علماء الفيزياء لا يقبلون بوجود عمليات في الطبيعة تحدث بسرعة اكبر من سرعة الضوء؛ اذ انهم يشيرون الى التعارض بين نظرية النسبية الخاصة ووجود هذه التفاعلات، كما يشيرون الى «نظرية عدم الاتصال»، وهي نتيجة مباشرة لميكانيكا الكم، لإرسال معلومات فعلية وقبلة للاستخدام بسرعة أكبر من سرعة الضوء. (لذا اذا كانت هنالك تأثيرات اسرع من الضوء تسهم بشكل ما في الاخلال بمتباينة بيل، فإنها ستكون مخفية بعيدا وربما بشكل تآمري؛ لكي لا نستطيع اكتشافها مباشرة.) أما كيف يمكن التوفيق بين استحالة ارسال إشارات بسرعة اكبر من الضوء وبين متباينة بيل والاخلال بها، فهذه مسألة خلافية وغير واضحة.
إن هذه الالغاز – مسألة القياس وتفسير الحالة الكمية، وطبيعة التشابك الكمي، وسمة اللامحلية التي يشير اليها الاخلال بمتباينة بيل – هي «حقائق موجودة بالفعل» لا بد أن تتناولها أي محاولة لفهم ميكانيكا الكم، وينبغي أن يكون واضحا بالفعل أن توفير امتداد بسيط لاطار الميكانيكا الكلاسيكية (أو الميكانيكا الإحصائية في الحقيقة) أ/مر مستبعد؛ فمن الجلي أن فهم ميكانيكا الكم يتطلب تغييرا في التوجه الفلسفي، أو في الفيزياء نفسها، أو في كليهما.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















