
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Measurement of position and momentum
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 38
2024-04-20
1976
Let us consider two examples of this idea—to see the reason why there is an uncertainty in the position and/or the momentum, if quantum mechanics is right. We have also seen before that if there were not such a thing—if it were possible to measure the position and the momentum of anything simultaneously—we would have a paradox; it is fortunate that we do not have such a paradox, and the fact that such an uncertainty comes naturally from the wave picture shows that everything is mutually consistent.
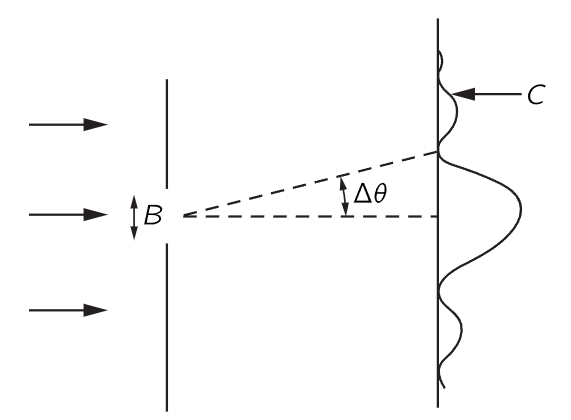
Fig. 38–2. Diffraction of particles passing through a slit.
Here is one example which shows the relationship between the position and the momentum in a circumstance that is easy to understand. Suppose we have a single slit, and particles are coming from very far away with a certain energy—so that they are all coming essentially horizontally (Fig. 38–2). We are going to concentrate on the vertical components of momentum. All of these particles have a certain horizontal momentum p0, say, in a classical sense. So, in the classical sense, the vertical momentum py, before the particle goes through the hole, is definitely known. The particle is moving neither up nor down, because it came from a source that is far away—and so the vertical momentum is of course zero. But now let us suppose that it goes through a hole whose width is B. Then after it has come out through the hole, we know the position vertically—the y position—with considerable accuracy—namely ±B. 1 That is, the uncertainty in position, Δy, is of order B. Now we might also want to say, since we know the momentum is absolutely horizontal, that Δpy is zero; but that is wrong. We once knew the momentum was horizontal, but we do not know it any more. Before the particles passed through the hole, we did not know their vertical positions. Now that we have found the vertical position by having the particle come through the hole, we have lost our information on the vertical momentum! Why? According to the wave theory, there is a spreading out, or diffraction, of the waves after they go through the slit, just as for light. Therefore, there is a certain probability that particles coming out of the slit are not coming exactly straight. The pattern is spread out by the diffraction effect, and the angle of spread, which we can define as the angle of the first minimum, is a measure of the uncertainty in the final angle.
How does the pattern become spread? To say it is spread means that there is some chance for the particle to be moving up or down, that is, to have a component of momentum up or down. We say chance and particle because we can detect this diffraction pattern with a particle counter, and when the counter receives the particle, say at C in Fig. 38–2, it receives the entire particle, so that, in a classical sense, the particle has a vertical momentum, in order to get from the slit up to C.
To get a rough idea of the spread of the momentum, the vertical momentum py has a spread which is equal to p0Δθ, where p0 is the horizontal momentum. And how big is Δθ in the spread-out pattern? We know that the first minimum occurs at an angle Δθ such that the waves from one edge of the slit have to travel one wavelength farther than the waves from the other side. Therefore, Δθ is λ/B, and so Δpy in this experiment is p0λ/B. Note that if we make B smaller and make a more accurate measurement of the position of the particle, the diffraction pattern gets wider. Remember, when we closed the slits on the experiment with the microwaves, we had more intensity farther out. So, the narrower we make the slit, the wider the pattern gets, and the more is the likelihood that we would find that the particle has sidewise momentum. Thus, the uncertainty in the vertical momentum is inversely proportional to the uncertainty of y. In fact, we see that the product of the two is equal to p0λ. But λ is the wavelength and p0 is the momentum, and in accordance with quantum mechanics, the wavelength times the momentum is Planck’s constant h. So we obtain the rule that the uncertainties in the vertical momentum and in the vertical position have a product of the order h:
Δy Δpy ≥ ℏ/2. (38.3)
We cannot prepare a system in which we know the vertical position of a particle and can predict how it will move vertically with greater certainty than given by (38.3). That is, the uncertainty in the vertical momentum must exceed ℏ/2Δy, where Δy is the uncertainty in our knowledge of the position.
Sometimes people say quantum mechanics is all wrong. When the particle arrived from the left, its vertical momentum was zero. And now that it has gone through the slit, its position is known. Both position and momentum seem to be known with arbitrary accuracy. It is quite true that we can receive a particle, and on reception determine what its position is and what its momentum would have had to have been to have gotten there. That is true, but that is not what the uncertainty relation (38.3) refers to. Equation (38.3) refers to the predictability of a situation, not remarks about the past. It does no good to say “I knew what the momentum was before it went through the slit, and now I know the position,” because now the momentum knowledge is lost. The fact that it went through the slit no longer permits us to predict the vertical momentum. We are talking about a predictive theory, not just measurements after the fact. So, we must talk about what we can predict.
Now let us take the thing the other way around. Let us take another example of the same phenomenon, a little more quantitatively. In the previous example we measured the momentum by a classical method. Namely, we considered the direction and the velocity and the angles, etc., so we got the momentum by classical analysis. But since momentum is related to wave number, there exists in nature still another way to measure the momentum of a particle—photon or otherwise—which has no classical analog, because it uses Eq. (38.2). We measure the wavelengths of the waves. Let us try to measure momentum in this way.

Fig. 38–3. Determination of momentum by using a diffraction grating.
Suppose we have a grating with a large number of lines (Fig. 38–3), and send a beam of particles at the grating. We have often discussed this problem: if the particles have a definite momentum, then we get a very sharp pattern in a certain direction, because of the interference. And we have also talked about how accurately we can determine that momentum, that is to say, what the resolving power of such a grating is. Rather than derive it again, where we found that the relative uncertainty in the wavelength that can be measured with a given grating is 1/Nm, where N is the number of lines on the grating and m is the order of the diffraction pattern. That is,
Δλ /λ = 1/Nm. (38.4)
Now formula (38.4) can be rewritten as
Δλ / λ2 = 1/Nmλ = 1/L, (38.5)
where L is the distance shown in Fig. 38–3. This distance is the difference between the total distance that the particle or wave or whatever it is has to travel if it is reflected from the bottom of the grating, and the distance that it has to travel if it is reflected from the top of the grating. That is, the waves which form the diffraction pattern are waves which come from different parts of the grating. The first ones that arrive come from the bottom end of the grating, from the beginning of the wave train, and the rest of them come from later parts of the wave train, coming from different parts of the grating, until the last one finally arrives, and that involves a point in the wave train a distance L behind the first point. So, in order that we shall have a sharp line in our spectrum corresponding to a definite momentum, with an uncertainty given by (38.4), we have to have a wave train of at least length L. If the wave train is too short, we are not using the entire grating. The waves which form the spectrum are being reflected from only a very short sector of the grating if the wave train is too short, and the grating will not work right—we will find a big angular spread. In order to get a narrower one, we need to use the whole grating, so that at least at some moment the whole wave train is scattering simultaneously from all parts of the grating. Thus, the wave train must be of length L in order to have an uncertainty in the wavelength less than that given by (38.5). Incidentally,
Δλ/λ2 = Δ(1/λ) = Δk/2π. (38.6)
Therefore
Δk = 2π/L, (38.7)
where L is the length of the wave train.
This means that if we have a wave train whose length is less than L, the uncertainty in the wave number must exceed 2π/L. Or the uncertainty in a wave number times the length of the wave train—we will call that for a moment Δx—exceeds 2π. We call it Δx because that is the uncertainty in the location of the particle. If the wave train exists only in a finite length, then that is where we could find the particle, within an uncertainty Δx. Now this property of waves, that the length of the wave train times the uncertainty of the wave number associated with it is at least 2π, is a property that is known to everyone who studies them. It has nothing to do with quantum mechanics. It is simply that if we have a finite train, we cannot count the waves in it very precisely. Let us try another way to see the reason for that.
Suppose that we have a finite train of length L; then because of the way it has to decrease at the ends, as in Fig. 38–1, the number of waves in the length L is uncertain by something like ±1. But the number of waves in L is kL/2π. Thus k is uncertain, and we again get the result (38.7), a property merely of waves. The same thing works whether the waves are in space and k is the number of radians per centimeter and L is the length of the train, or the waves are in time and ω is the number of radians per second and T is the “length” in time that the wave train comes in. That is, if we have a wave train lasting only for a certain finite time T, then the uncertainty in the frequency is given by
Δω = 2π/T. (38.8)
We have tried to emphasize that these are properties of waves alone, and they are well known, for example, in the theory of sound.
The point is that in quantum mechanics we interpret the wave number as being a measure of the momentum of a particle, with the rule that p=ℏk, so that relation (38.7) tells us that Δp ≈ h/Δx. This, then, is a limitation of the classical idea of momentum. (Naturally, it has to be limited in some ways if we are going to represent particles by waves!) It is nice that we have found a rule that gives us some idea of when there is a failure of classical ideas.
_____________________________________________
Margin
1- More precisely, the error in our knowledge of y is ±B/2. But we are now only interested in the general idea, so we won’t worry about factors of 2
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















