As Lagrange showed, any irrational number 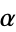 has an infinity of rational approximations  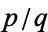which satisfy

(1)

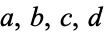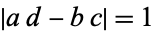Furthermore, if there are no integers  with  and 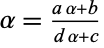 (corresponding to values of  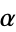associated with the golden ratio  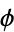through their continued fractions), then

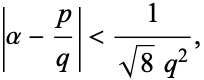(2)

and if values of 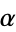 associated with the silver ratio  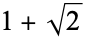are also excluded, then

(3)

In general, even tighter bounds of the form

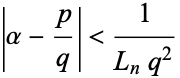(4)

can be obtained for the best rational approximation possible for an arbitrary irrational number 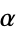, where the  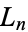are called Lagrange numbers and get steadily larger for each "bad" set of irrational numbers which is excluded.

REFERENCES:

Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, p. 145, 1997.

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 40, 1987.

Chandrasekharan, K. An Introduction to Analytic Number Theory. Berlin: Springer-Verlag, p. 23, 1968.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 187-189, 1996.