Dedekind Sum
المؤلف:
Apostol, T. M.
المصدر:
Ch. 12 in Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
الجزء والصفحة:
...
17-8-2020
2690
Dedekind Sum
Given relatively prime integers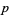 
and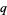 
(i.e., 
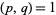), the Dedekind sum is defined by
 |
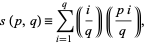(1)
|
where
![((x))=<span style=]() {x-|_x_|-1/2 x not in Z; 0 x in Z, " src="https://mathworld.wolfram.com/images/equations/DedekindSum/NumberedEquation2.gif" style="height:48px; width:166px" /> |
(2)
|
with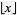 
the floor function. 
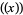is an odd function since 
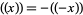and is periodic with period 1. The Dedekind sum is meaningful even if 
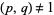, so the relatively prime restriction is sometimes dropped (Apostol 1997, p. 72). The symbol 
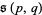is sometimes used instead of 
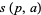(Beck 2000).
The Dedekind sum can also be expressed in the form
 |
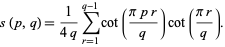(3)
|
If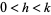 
, let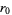 
, 
, ..., 
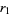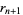denote the remainders in the Euclidean algorithm given by
for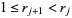 
and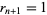 
. Then
![s(h,k)=1/(12)sum_(j=1)^(n+1)<span style=]() {(-1)^(j+1)(r_j^2+r_(j-1)^2+1)/(r_jr_(j-1))}-((-1)^n+1)/8 " src="https://mathworld.wolfram.com/images/equations/DedekindSum/NumberedEquation4.gif" style="height:50px; width:307px" /> |
(7)
|
(Apostol 1997, pp. 72-73).
In general, there is no simple formula for closed-form evaluation of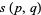 
, but some special cases are
(Apostol 1997, p. 62). Apostol (1997, p. 73) gives the additional special cases
 |
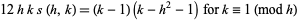(10)
|
![12hks(h,k)=(k-2)[k-1/2(h^2+1)] for k=2 (mod h)](https://mathworld.wolfram.com/images/equations/DedekindSum/NumberedEquation6.gif) |
(11)
|
 |
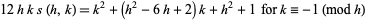(12)
|
 |
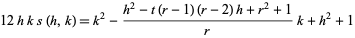(13)
|
for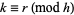 
and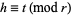 
, where 
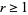and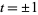 
. Finally,
 |
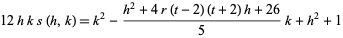(14)
|
for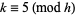 
and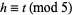 
, where 
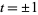or 
.
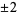Dedekind sums obey 2-term
 |
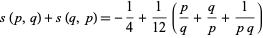(15)
|
(Dedekind 1953; Rademacher and Grosswald 1972; Pommersheim 1993; Apostol 1997, pp. 62-64) and 3-term
 |
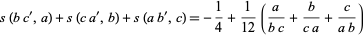(16)
|
(Rademacher 1954), reciprocity laws, where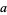 
, 
; 
, 
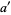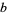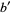; and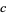 
, 
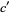are pairwise relatively prime, and
(Pommersheim 1993).
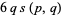is an integer (Rademacher and Grosswald 1972, p. 28), and if 
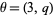, then
 |
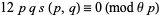(20)
|
and
 |
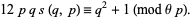(21)
|
In addition,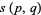 
satisfies the congruence
 |
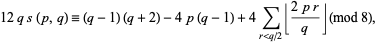(22)
|
which, if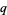 
is odd, becomes
 |
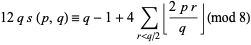(23)
|
(Apostol 1997, pp. 65-66). If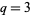 
, 5, 7, or 13, let 
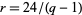, let integers 
, 
, 
, 
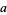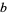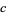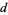be given with 
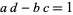such that 
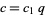and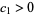 
, and let
![delta=<span style=]() {s(a,c)-(a+d)/(12c)}-{s(a,c_1)-(a+d)/(12c_1)}. " src="https://mathworld.wolfram.com/images/equations/DedekindSum/NumberedEquation16.gif" style="height:38px; width:256px" /> |
(24)
|
Then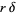 
is an even integer (Apostol 1997, pp. 66-69).
Let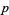 
, 
, 
, 
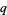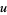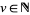with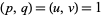 
(i.e., are pairwise relatively prime), then the Dedekind sums also satisfy
 |
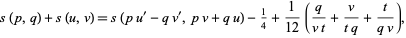(25)
|
where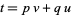 
, and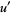 
, 
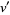are any integers such that 
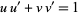(Pommersheim 1993).
If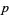 
is prime, then
 |
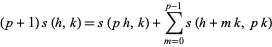(26)
|
(Dedekind 1953; Apostol 1997, p. 73). Moreover, it has been beautifully generalized by Knopp (1980).
REFERENCES:
Apostol, T. M. "Properties of Dedekind Sums," "The Reciprocity Law for Dedekind Sums," and "Congruence Properties of Dedekind Sums." §3.7-3.9 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 52 and 61-69, 1997.
Apostol, T. M. Ch. 12 in Introduction to Analytic Number Theory. New York: Springer-Verlag, 1976.
Beck, M. "Dedekind Cotangent Sums" 7 Dec 2001. https://arxiv.org/abs/math.NT/0112077.
Dedekind, R. "Erlauterungen zu den Fragmenten, XXVIII." In The Collected Works of Bernhard Riemann. New York: Dover, pp. 466-478, 1953.
Iseki, S. "The Transformation Formula for the Dedekind Modular Function and Related Functional Equations." Duke Math. J. 24, 653-662, 1957.
Knopp, M. I. "Hecke Operators and an Identity for Dedekind Sums." J. Number Th. 12, 2-9, 1980.
Pommersheim, J. "Toric Varieties, Lattice Points, and Dedekind Sums." Math. Ann. 295, 1-24, 1993.
Rademacher, H. "Generalization of the Reciprocity Formula for Dedekind Sums." Duke Math. J. 21, 391-398, 1954.
Rademacher, H. and Grosswald, E. Dedekind Sums. Washington, DC: Math. Assoc. Amer., 1972.
Rademacher, H. and Whiteman, A. L. "Theorems on Dedekind Sums." Amer. J. Math. 63, 377-407, 1941.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
