Hyperfactorial
المؤلف:
Fletcher, A.; Miller, J. C. P.; Rosenhead, L.; and Comrie, L. J
المصدر:
An Index of Mathematical Tables, Vol. 1, 2nd ed. Reading, MA: Addison-Wesley
الجزء والصفحة:
...
23-11-2018
888
Hyperfactorial
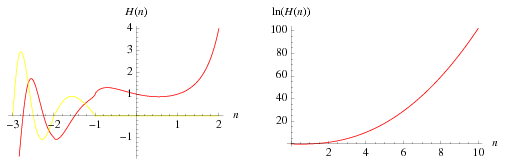
The hyperfactorial (Sloane and Plouffe 1995) is the function defined by
where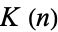 
is the K-function.
The hyperfactorial is implemented in the Wolfram Language as Hyperfactorial[n].
For integer values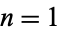 
, 2, ... are 1, 4, 108, 27648, 86400000, 4031078400000, 3319766398771200000, ... (OEIS A002109).
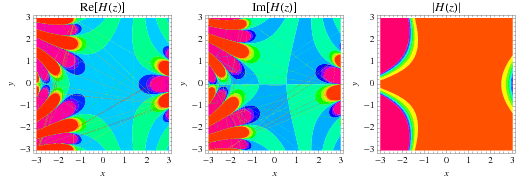
The hyperfactorial can also be generalized to complex numbers, as illustrated above.
The Barnes G-function and hyperfactorial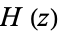 
satisfy the relation
 |
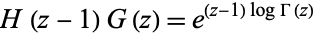(3)
|
for all complex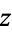 
.
The hyperfactorial is given by the integral
![H(z)=(2pi)^(-z/2)exp[(z+1; 2)+int_0^zln(t!)dt]](http://mathworld.wolfram.com/images/equations/Hyperfactorial/NumberedEquation2.gif) |
(4)
|
and the closed-form expression
 |
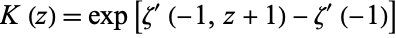(5)
|
for ![R[z]>0](http://mathworld.wolfram.com/images/equations/Hyperfactorial/Inline11.gif)
, where 
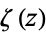is the Riemann zeta function, 
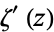its derivative, 
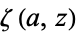is the Hurwitz zeta function, and
 |
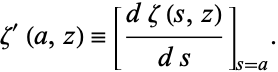(6)
|
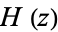also has a Stirling-like series
 |
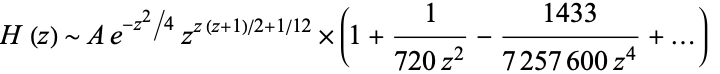(7)
|
(OEIS A143475 and A143476).
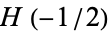has the special value
where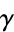 
is the Euler-Mascheroni constant and 
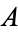is the Glaisher-Kinkelin constant.
The derivative is given by
![(dH(x))/(dx)=H(x)<span style=]() {1/2[1-ln(2pi)]+ln(Gamma(x+1))+x}. " src="http://mathworld.wolfram.com/images/equations/Hyperfactorial/NumberedEquation6.gif" style="height:35px; width:297px" /> |
(11)
|
REFERENCES:
Fletcher, A.; Miller, J. C. P.; Rosenhead, L.; and Comrie, L. J. An Index of Mathematical Tables, Vol. 1, 2nd ed. Reading, MA: Addison-Wesley, p. 50, 1962.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 477, 1994.
Sloane, N. J. A. Sequences A002109/M3706, A143475, and A143476 in "The On-Line Encyclopedia of Integer Sequences."
الاكثر قراءة في التحليل العقدي
اخر الاخبار
اخبار العتبة العباسية المقدسة
