Meromorphic Function
المؤلف:
Knopp, K
المصدر:
"Meromorphic Functions." Ch. 2 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover,
الجزء والصفحة:
...
18-10-2018
1025
Meromorphic Function
A meromorphic function is a single-valued function that is analytic in all but possibly a discrete subset of its domain, and at those singularities it must go to infinity like a polynomial (i.e., these exceptional points must be poles and not essential singularities). A simpler definition states that a meromorphic function is a function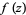 
of the form
where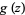 
and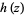 
are entire functions with 
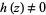(Krantz 1999, p. 64).
A meromorphic function therefore may only have finite-order, isolated poles and zeros and no essential singularities in its domain. A meromorphic function with an infinite number of poles is exemplified by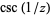 
on the punctured disk ![U=D<span style=]()
{0}" src="http://mathworld.wolfram.com/images/equations/MeromorphicFunction/Inline6.gif" style="height:14px; width:60px" />, where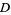 
is the open unit disk.
An equivalent definition of a meromorphic function is a complex analytic map to the Riemann sphere.
The word derives from the Greek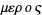 
(meros), meaning "part," and 
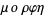(morphe), meaning "form" or "appearance."
REFERENCES:
Knopp, K. "Meromorphic Functions." Ch. 2 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 34-57, 1996.
Krantz, S. G. "Meromorphic Functions and Singularities at Infinity." §4.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 63-68, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 382-383, 1953.
الاكثر قراءة في التحليل العقدي
اخر الاخبار
اخبار العتبة العباسية المقدسة
