Floquet Analysis
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
12-6-2018
1415
Floquet Analysis
Given a system of ordinary differential equations of the form
![d/(dt)[x; y; v_x; v_y]=-[0 0 -1 0; 0 0 0 -1; Phi_(xx)(t) Phi_(yx)(t) 0 0; Phi_(xy)(t) Phi_(yy)(t) 0 0][x; y; v_x; v_y]](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/NumberedEquation1.gif) |
(1)
|
that are periodic in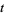 
, the solution can be written as a linear combination of functions of the form
![[x(t); y(t); v_x(t); v_y(t)]=[x_0; y_0; v_(x0); v_(y0)]e^(mut)P_mu(t),](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/NumberedEquation2.gif) |
(2)
|
where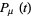 
is a function periodic with the same period 
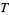as the equations themselves. Given an ordinary differential equation of the form
 |
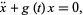(3)
|
where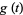 
is periodic with period 
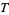, the ODE has a pair of independent solutions given by the real and imaginary parts of
Plugging these into (◇) gives
 |
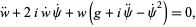(8)
|
so the real and imaginary parts are
 |
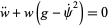(9)
|
 |
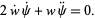(10)
|
From (◇),
Integrating gives
 |
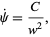(14)
|
where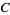 
is a constant which must equal 1, so 
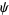is given by
 |
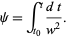(15)
|
The real solution is then
![x(t)=w(t)cos[psi(t)],](http://mathworld.wolfram.com/images/equations/FloquetAnalysis/NumberedEquation9.gif) |
(16)
|
so
and
which is an integral of motion. Therefore, although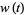 
is not explicitly known, an integral 
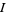always exists. Plugging (◇) into (◇) gives
 |
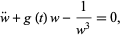(25)
|
which, however, is not any easier to solve than (◇).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 727, 1972.
Binney, J. and Tremaine, S. Galactic Dynamics. Princeton, NJ: Princeton University Press, p. 175, 1987.
Lichtenberg, A. and Lieberman, M. Regular and Stochastic Motion. New York: Springer-Verlag, p. 32, 1983.
Margenau, H. and Murphy, G. M. The Mathematics of Physics and Chemistry, 2 vols. Princeton, NJ: Van Nostrand, 1956-64.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 556-557, 1953.
الاكثر قراءة في معادلات تفاضلية
اخر الاخبار
اخبار العتبة العباسية المقدسة
