Mobility Effects

In the last section, we defined mobility, which relates the average drift velocity of a carrier to the electric field. Electron and hole mobilities are important semiconductor parameters in the characterization of carrier drift.

Equation (1) related the acceleration of a hole to a force such as an electric held.

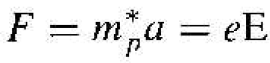(1)

We may write this equation as

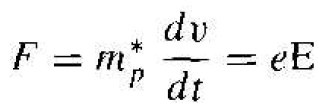(2)

where v is the velocity of the particle due to the electric field and does not include the random thermal velocity. If we assume that the effective mass and electric field are constants, then we may integrate Equation (2) and obtain

(3)

where we have assumed the initial drift velocity to be zero.

Figure 1.la shows a schematic model of the random thermal velocity and motion of a hole in a semiconductor with zero electric field. There is a mean time between collisions which may be denoted by τ_cp. If a small electric field (E-field) is

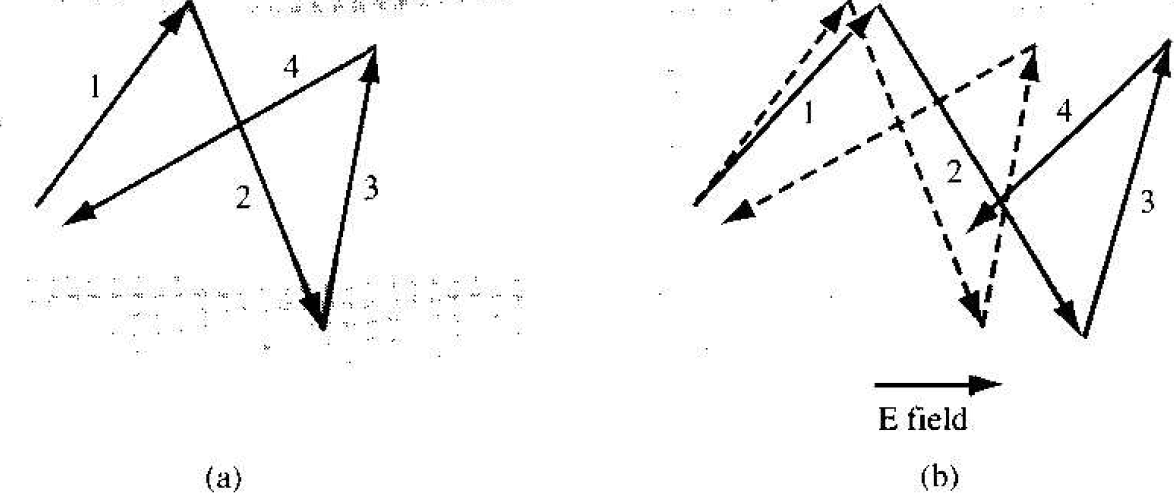
Figure 1.1 Typical random behavior of a hole in a semiconductor (a) without an electric field and (b) with an electric field.

applied as indicated in Figure 1.lb, there will be a net drift of the hole in the direction of the E-field, and the net drift velocity will be a small perturbation on the random thermal velocity, so the time between collisions will not be altered appreciably. If we use the mean time between collisions τ_cp in place of the time t in Equation (3), then the mean peak velocity just prior to a collision or scattering event is

(4a)

The average drift velocity is one half the peak value so that we can write

(4b)

However, the collision process is not as simple as this model, but is statistical in nature. In a more accurate model including the effect of a statistical distribution, the factor 1/2 in Equation (1.4b) does not appear. The hole mobility is then give by

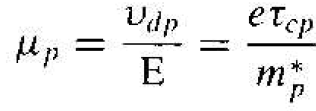(5)

The same analysis applies to electrons; thus we can write the electron mobility as

(6)

where τ_cn is the mean time between collisions for an electron.

There are two collision or scattering mechanisms that dominate in a semiconductor and affect the carrier mobility: phonon or lattice scattering, and ionized impurity scattering.

The atoms in a semiconductor crystal have a certain amount of thermal energy at temperatures above absolute zero that causes the atoms to randomly vibrate about their lattice position within the crystal. The lattice vibrations cause a disruption in  perfect periodic potential function. A perfect periodic potential in a solid allows electrons to move unimpeded, or with no scattering, through the crystal. But the thermal vibrations cause a disruption of the potential function, resulting in an interaction between the electrons or holes and the vibrating lattice atoms. This lattice scattering is also referred to as phonon scattering.

Since lattice scattering is related to the thermal motion of atoms, the rate at which the scattering occurs is a function of temperature. If we denote μ_L as the mobility that would be observed if only lattice scattering existed, then the scattering theory states that to first order

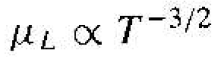(6)

Mobility that is due to lattice scattering increases as the temperature decreases. Intuitively, we expect the lattice vibrations to decrease as the temperature decreases, which implies that the probability of a scattering event also decreases, thus increasing mobility.

Figure 1.2 is a plot of electron and hole mobilities in germanium, silicon, and gallium arsenide at T = 300 K as a function of impurity concentration. More accurately, these curves are of mobility versus ionized impurity concentration N_I. As the impurity concentration increases, the number of impurity scattering centers increases, thus reducing mobility.

Figure 1.2 Electron and hale mobilities versus impurity concentrations for germanium, silicon. and gallium arsenide at T = 300 K.

then dt /τ_I is the probability of an ionized impurity scattering event occurring in the differential time dt. If these two scattering processes are independent, then the total probability of a scattering event occurring in the differential time dt is the sum of the individual events, or

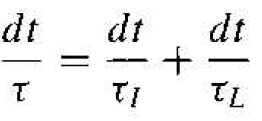(7)

where τ is the mean time between any scattering event.

Comparing Equation (7) with the definitions of mobility given by Equation (5) or (6), we can write

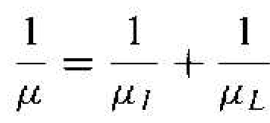(8)

where μ_I is the mobility due to the ionized impurity scattering process and μ_L is the mobility due to the lattice scattering process. The parameter μ is the net mobility. With two or more independent scattering mechanisms, the inverse mobilities add which means that the net mobility decreases.