Ionization Energy

We can calculate the approximate distance of the donor electron from the donor impurity ion, and also the approximate energy required to elevate the donor electron into the conduction band. This energy is referred to as the ionization energy. We will use the Bohr model of the atom for these calculations. The justification for using this model is that the most probable distance of an electron from the nucleus in a hydrogen atom, determined from quantum mechanics, is the same as the Bohr radius. The energy levels in the hydrogen atom determined from quantum mechanics are also the same as obtained from the Bohr theory.

In the case of the donor impurity atom, we may visualize the donor electron orbiting the donor ion, which is embedded in the semiconductor material. We will need to use the permittivity of the semiconductor material in the calculations rather than the permittivity of free space as is used in the case of the hydrogen atom. We will all use the effective mass of the electron in the calculations.

The analysis begins by setting the coulomb force of attraction between the electron and ion equal to the centripetal force of the orbiting electron. This condition we give a steady orbit. We have

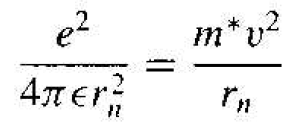(1)

where v is the magnitude of the velocity and r_n is the radius of the orbit. If we assort the angular momentum is also quantized, then we can write

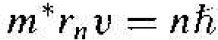(2)

where n is a positive integer. Solving for v from Equation (2), substituting in Equation (1), and solving for the radius, we obtain

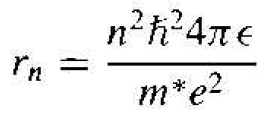(3)

The assumption of the angular momentum being quantized leads to the radius as being quantized.

The Bohr radius is defined as

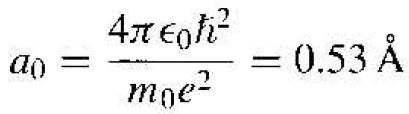(4)

We can normalize the radius of the donor orbital to that of the Bohr radius, which give

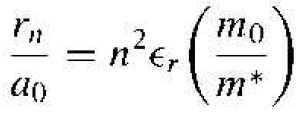(5)

where ϵ_r is the relative dielectric constant of the semiconductor material, m₀ is tires mass of an electron, and m* is the conductivity effective mass of and m^* is the conductivity effective mass of the electron the electron the semiconductor.

If we consider the lowest energy state in which n = 1, and if we consider silos in which ϵ_r = 11.7 and the conductivity effective mass is m^*/m₀ = 0.26. then we have that

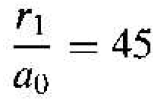(6)

or r₁ = 23.9 A. This radius corresponds to approximately four lattice constants silicon. Recall that one unit cell in silicon effectively contains eight atoms, so the radius of the orbiting donor electron encompasses many silicon atoms. The donor electron is not tightly bound to the donor atom.

The total energy of the orbiting electron is given by

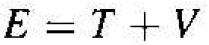(7)

where T is the kinetic energy and V is the potential energy of the electron. The kinetic energy is

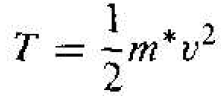(8)

Using the velocity v from Equation (2) and the radius r_n from Equation (3), the kinetic energy becomes

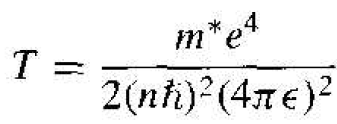(9)

The potential energy is

(10)

The total energy is the sum of the kinetic and potential energies, so that

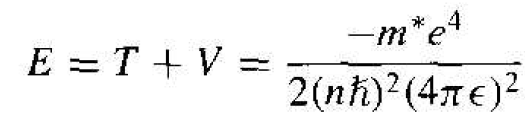(11)

For the hydrogen atom, m^* = m₀ and ϵ = ϵ₀. The ionization energy of the hydrogen atom in the lowest energy state is then E = - 13.6 eV. If we consider silicon, the ionization energy is E = -25.8 m eV, much less than the bandgap energy of silicon. This energy is the approximate ionization energy of the donor atom, or the energy required to elevate the donor electron into the conduction band.

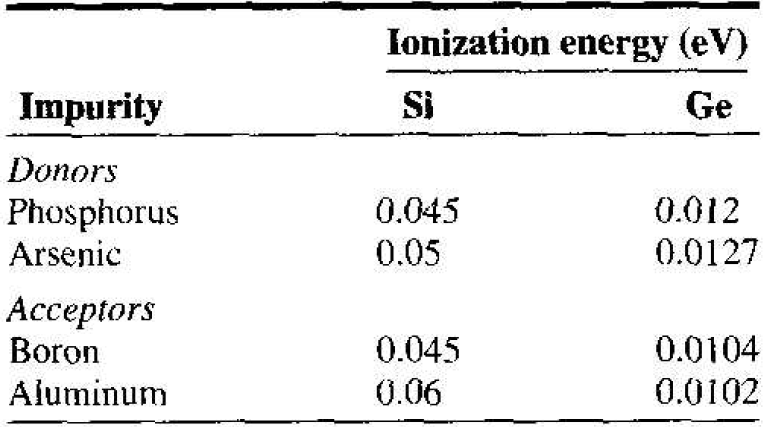
For ordinary donor impurities such as phosphorus or arsenic in silicon or germanium, this hydrogenic model works quite well and gives some indication of the magnitudes of the ionization energies involved. Table 1.1 lists the actual experimentally measured ionization energies for a few impurities in silicon and germanium. Germanium and silicon have different relative dielectric constants and effective masses; thus we expect the ionization energies to differ.

Table 1.1 Impurity ionization energies in silicon and germanium.