
Primitive and Unit Cell
 المؤلف:
Donald A. Neamen
المؤلف:
Donald A. Neamen
 المصدر:
Semiconductor Physics and Devices
المصدر:
Semiconductor Physics and Devices
 الجزء والصفحة:
p 3
الجزء والصفحة:
p 3
 8-5-2017
8-5-2017
 3977
3977
Primitive and Unit Cell
We can represent a particular atomic array by a dot that is called a lattice point. Figure 1.1 shows an infinite two-dimensional array of lattice points. The simplest means of repeating an atomic array is by translation. Each lattice point in Figure 1.1 can be translated a distance a1 in one direction and a distance b1 in a second non-colinear direction to generate the two-dimensional lattice. A third non-colinear translation will produce the three-dimensional lattice. The translation directions need not be perpendicular.
Since the three-dimensional lattice is a periodic repetition of a group of atoms, we do not need to consider the entire lattice, but only a fundamental unit that is being repeated. A unit cell is a small volume of the crystal that can be used to reproduce the entire crystal. A unit cell is not a unique entity. Figure 1.2 shows several possible unit cells in a two-dimensional lattice.
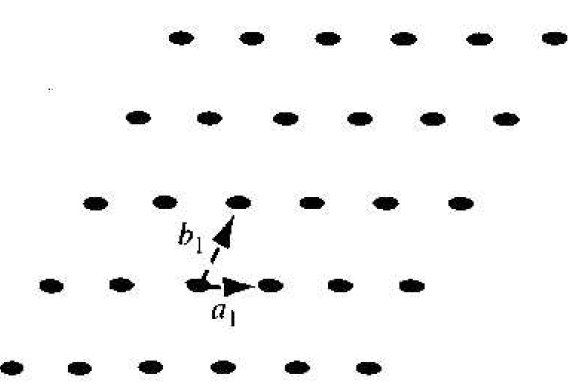
Figure 1.1 Two-dimensional representation of a single-crystal lattice.

Figure 1.2 Two-dimensional representation of a single-crystal lattice showing various possible unit cells.

Figure 1.3 A generalized primitive unit cell.
The unit cell A can be translated in directions a2 and b2, the unit cell B can be translated in directions a3 and b3, and the entire two-dimensional lattice can be constructed by the translations of either of these unit cells. The unit cells C and D in Figure 1.2 can also be used to construct the entire lattice by using the appropriate translations. This discussion of two-dimensional unit cells can easily be extended to three dimensions to describe a real single-crystal material.
A primitive cell is the smallest unit cell that can be repeated to form the lattice. In many cases, it is more convenient to use a unit cell that is not a primitive cell. Unit cells may be chosen that have orthogonal sides, thr example, whereas the sides of a primitive cell may be non-orthogonal.
A generalized three-dimensional unit cell is shown in Figure 1.3. The relationship between this cell and the lattice is characterized by three vectors 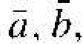 and
and  which need not be perpendicular and which may or may not be equal in length. Every equivalent lattice point in the three-dimensional crystal can be found using the vector
which need not be perpendicular and which may or may not be equal in length. Every equivalent lattice point in the three-dimensional crystal can be found using the vector
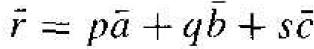 (1)
(1)
where p, q, and s are integers. Since the location of the origin is arbitrary, we will let p. q, and s be positive integers for simplicity.
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


