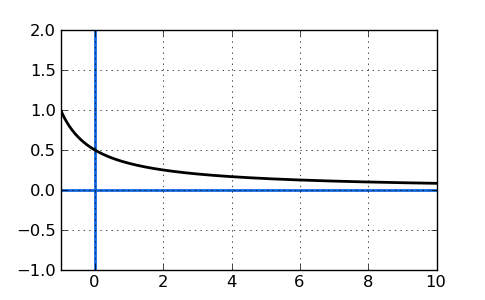
To find horizontal asymptotes, we may write the function in the form of "y=". You can expect to find horizontal asymptotes when you are plotting a rational function, such as: y=x3+2x2+92x3−8x+3. Horizontal asymptotes occur when the graph of the function grows closer and closer to a particular value without ever actually reaching that value as x gets very positive or very negative.

To Find Horizontal Asymptotes:

1) Put equation or function in y= form.

2) Multiply out (expand) any factored polynomials in the numerator or denominator.

3) Remove everything except the terms with the biggest exponents of x found in the numerator and denominator. These are the "dominant" terms.

Sample A: Find the horizontal asymptotes of:

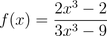
Remember that horizontal asymptotes appear as x extends to positive or negative infinity, so we need to figure out what this fraction approaches as x gets huge. To do that, we'll pick the "dominant" terms in the numerator and denominator. Dominant terms are those with the largest exponents. As x goes to infinity, the other terms are essentially meaningless.

The largest exponents in this case are the same in the numerator and denominator (3). The dominant terms in each have an exponent of 3. Get rid of the other terms and then simplify by crossing-out the x3 in the top and bottom:

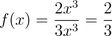
In this case, 2/3 is the horizontal asymptote of the above function. You should actually express it as y=2/3. This value is the asymptote because when we approach x=infinity, the "dominant" terms will dwarf the rest and the function will always get closer and closer to y=2/3. Here's a graph of that function as a final illustration that this is correct:

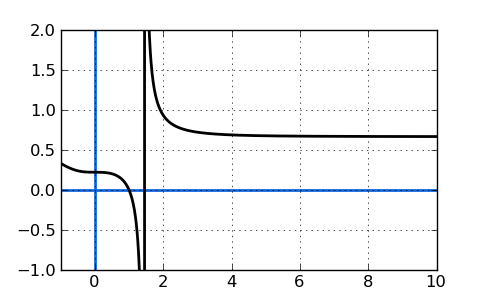
(Notice that there's also a vertical asymptote present in this function.)

If the exponent in the denominator of the function is larger than the exponent in the numerator, the horizontal asymptote will be y=0, which is the x-axis. As x approaches positive or negative infinity, that denominator will be much, much larger than the numerator (infinitely larger, in fact) and will make the overall fraction equal zero.

If there is a bigger exponent in the numerator of a given function, then there is NO horizontal asymptote. For example:

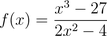
There will be NO horizontal asymptote(s) because there is a BIGGER exponent in the numerator, which is 3. See it? This will make the function increase forever instead of closely approaching an asymptote. The plot of this function is below. Note that again there are also vertical asymptotespresent on the graph.

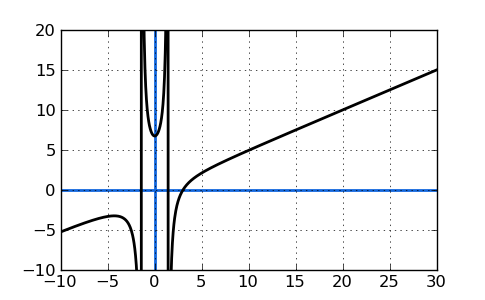
Sample B: Find the horizontal asymptotes of:

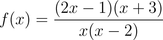
In this sample, the function is in factored form. However, we must convert the function to standard form as indicated in the above steps before Sample A. That means we have to multiply it out, so that we can observe the dominant terms.

Sample B, in standard form, looks like this:

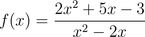
Next: Follow the steps from before. We drop everything except the biggest exponents of x found in the numerator and denominator. After doing so, the above function becomes:

Cancel x2 in the numerator and denominator and we are left with 2. Our horizontal asymptote for Sample B is the horizontal line y=2.