The interior Schwarzschild solution and the TOV equation

In the previous section we investigated the gravitational field outside a spherically symmetric mass distribution. Now it is time to have a look inside matter. Of course, in a first attempt, we have to make decisive simplifications on the internal structure of a star. We will consider cold catalyzed stellar material during the later phase of its evolution which can be reasonably approximated by a perfect fluid. The typical mass densities are in the range of ≈10⁷ g cm⁻³ (white dwarfs) or ≈10¹⁴ g cm⁻³ (neutron stars, i.e. pulsars). In this context we assume vanishing angular momentum.

We start again from a static and spherically symmetric metric

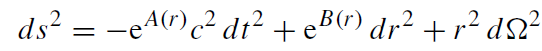 (1.1)

and the energy–momentum tensor

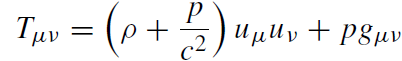 (1.2)

where ρ = ρ(r ) is the spherically symmetric mass density and p = p(r ) the pressure (isotropic stress). This has to be supplemented by the equation of state which, for a simple fluid, has the form p = p(ρ). We compute the non-vanishing components of the field equation by means of computer algebra as (here ()' = d/dr)

 (1.3)

 (1.4)

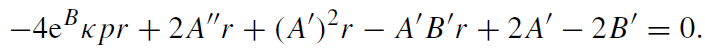 (1.5)

The (φ, φ)-component turns out to be equivalent to the (θ, θ)-component. For convenience, we define a mass function m(r) according to

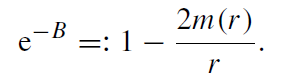 (1.6)

We can differentiate (1.6) with respect to r and find, after substituting (1.3), a differential equation for m(r) which can be integrated, provided ρ(r) is assumed to be known:

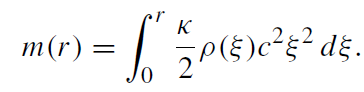 (1.7)

Differentiating (1.4) and using all three components of the field equation, we obtain a differential equation for A:

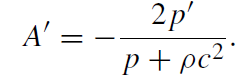 (1.8)

We can derive an alternative representation of A' by substituting (1.6) into (1.4). Then, together with (1.8), we arrive at the Tolman–Oppenheimer–Volkoff (TOV) equation

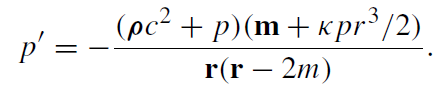 (1.9)

The Newtonian terms are denoted by boldface letters. The system of equations consisting of (1.7), (1.8), the TOV equation (1.9), and the equation of state p = p(ρ) forms a complete set of equations for the unknown functions A(r ), ρ(r), p(r ), and m(r ), with

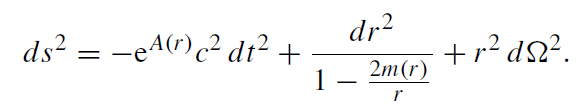 (1.10)

These differential equations have to be supplemented by initial conditions.

In the center of the star, there is, of course, no enclosed mass. Hence we demand m(0) = 0. The density has to be finite at the origin, i.e. ρ(0) = ρ_c, where ρ_c is the density of the central region. At the surfaces of the star, at r = R_ּ, we have to match matter with vacuum. In vacuum, there is no pressure which requires p(R_ּ) = 0. Moreover, the mass function should then yield the total mass of the star, m(R_ּ) = M. Finally, we have to match the components of the metric. Therefore, we have to demand exp[A(R_ּ)] = 1 − 2m(R_ּ)/R_ּ.

Equations (1.3), (1.4), (1.5) and certain regularity conditions which generalize our boundary conditions, i.e.

● the regularity of the geometry at the origin,

● the finiteness of the central pressure and density,

● the positivity of the central pressure and density,

● the positivity of the pressure and density,

● the monotonic decrease in pressure and density,

impose conditions on the functions ρ and p. Then, even without explicit knowledge of the equation of state, the general form of the metric can be determined. For most recent work, see Harman and Visser and the literature given there.

We can obtain a simple solution, if we assume a constant mass density

ρ = ρ(r ) = constant.   (1.11)

One should mention here that ρ is not the physically observable fluid density, which results from an appropriate projection of the energy–momentum tensor into the reference frame of an observer. Thus, this model is not as unphysical as it may look at first. However, there are serious but more subtle objections which we will not discuss further in this context. When ρ = constant, we can immediately integrate (1.6) and thus obtain the metric component exp(B). Also (1.8) can be integrated. Then, after some more elementary integrations, we can make use of the boundary conditions. Finally, we arrive at the interior and exterior Schwarzschild solution for a spherically symmetric body:

 (1.12)

with

 (1.13)

For the sun we have M_ּ ≈ 2 × 10³⁰ kg, R_ּ ≈ 7 × 10⁸ m and subsequently ρ_ּ ≈ 1.4×10³ kg m⁻³. This leads to ˆR ≈ 3×10¹¹, i.e. the radius of the star R_ּ is much smaller than ˆR : R_ּ < ˆR . Hence the square roots in (1.12) remain real.

اخر الاخبار

اخبار العتبة العباسية المقدسة

خمسون عامًا من العطاء.. نجم الأعرجي خادم الزائرين بلا انقطاع

العتبة العباسية المقدسة تواصل إقامة مجالسها العزائية لإحياء شهر المحرم

العتبة العباسية المقدسة تطلق سلسلة محاضرات قرآنية عاشورائية في بابل

في مساء اليوم الخامس من المحرّم.. المواكب الكربلائيّة تواصل فعالياتها العزائية

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

ثورة النسبية المكان والزمان في أزمة

التأثير في الزمن: ثبات سرعة الضوء وتهاوي المفهوم المطلق للزمن

أبعاد أكثر مما تراه العين

النسبية العامة في مواجهة ميكانيكا الكم

المكان والزمان وعين الراصد

هل هي موجة أم جسيمة؟

الحاجة إلى نظرية جديدة النسبية العامة في مواجهة ميكانيكا الكم

(التأثير في الزمن) تأثير الحركة على مرور الزمن: الساعة الضوئية وتباطؤ الزمن

الحركة خلال الزمكان (Spacetime)

تموجات في نسيج الزمكان: حين لحقت الجاذبية بالضوء (حل التناقض)

مرة أخرى اعوجاج الزمان(حين يتباطأ الزمن تحت ثقل الجاذبية)

التسارع واعوجاج المكان والزمان