الهندسة الهذلوليه
المؤلف:
ص27
المصدر:
نظرية النسبية العامة لأنشتاين
الجزء والصفحة:
جلال الحاج عبد
2025-10-22
21
لا تستطرق الهندسة للأشعة الضوئية، لكن مسير شعاع ضوئي يمكن أن يكون الطبيعة المادية الاصطلاح هندسي غير معرف كالخط. يذكر هرمان وائل (Hermann Werl) أن الذهن الرياضي حر وملزم، وهناك أحساس عند الرياضيين (علماء الرياضيات) و هو أنهم يتمتعون بحرية تعريف الاصطلاحات ووضع المسلمات، لكن المسائلة هي مدى توفقهم بأرضاء زملائهم الرياضيين بنتائج إحساساتهم وتخيلاتهم. لا يمكن الوقوف أمام هذه الإحساسات والكثير من البنى الرياضية هي حصيلة جهد و مساعي الأسرة الرياضية بأكملها، وقد أكدوا على استلزامها.
لا تخلو دنيا الرياضيات من الجدل حول النظم الموضوعات يه على رغم النتائج المثمرة التي جاءت بها هذه النظم، لقد نالت مسلمات كانتور في المجموعات اللا متناهيه جدلاً ورفضاً من أبرز الرياضيين (أمثال وايل وبرائور وبیشاب) و منهم من رفض جميع هذه المسلمات. إذا كانت هذه المسلمات هي أحكام صوريه لا معنى لها فلماذا نالت موافقة ومخالفة الكثيرين؟ هل هناك اعتراض على قواعد لعبة الشطرنج؟ النظرة الصورية على الرياضيات هي إنها لعبة صورية، هذه النظرة هي . منفذ للهروب من المسائلة الفلسفية و النفسية المعقدة لماهيات الإبداعات والاكتشافات الرياضية. في الحقيقة عندما يثق الرياضي بوجود شئ ماذا يقول؟ عندما أكتشف الفيثاغورثيون بأن وتر المثلث القائم الزاويه المتساوي و الساقين لا يمكن قياسه بنفس وحدة القياس التي يقاس بها الساقين عمدوا على كتمان اكتشافهم هذا أطلقوا التسمية على كهذا الطول بالأصم. أما نحن اليوم فلسنا مستائين من الأعداد الصماء كالعدد 2 بل ذهبنا الى أبعد من هذا بقبولنا الأعداد الخيالية التي جاء بها كاردان (Cardan) و ذلك من خلال إدخاله مفهوم 1- دنيا الرياضيات من المواضيع الأصوليه (fundamentalist) في فلسفة الرياضيات لكرونكر(Kroncker) مقولته الله الذي خلق الأعداد الصحيحة و بقية الأعداد هي من خلق الإنسان.
أكثر الرياضيين هم متفقون اليوم على مسلمات كانتور في المجموعات ويعتبرونها أساس الرياضيات. هناك سر في الرياضيات و هو إذا كانت الأبداعات الرياضيه هي حصيلة أوهام و تخيلات الرياضيين، فكيف يمكن لبعضها أن تتخذ طابع فيزيائي عملي؟ كالطابع العملي الذي اتخذته قوانين الحركه المداريه المستلهمة من المخروطات (كالشلجمي) والمعتمدة على مسلمات الهندسة التي وضعها اليونانيون، وكانت نتائجها هبوط الإنسان على سطح القمر ، لن يتصوروا بأن مسلماتهم هذه ستأخذ طابع عملي في غزو الفضاء!
الهدف من طرح هذا الموضوع هو ليس لإيذائكم وإنما لنبين لكم أن الرياضيات حية ودائماً في تغير ولا تنتهي. تدخل الى بحث الهندسه الهذلوليه بتعريفها وأهم مفاهيما وقضاياها.
كل هندسه غير إقليديه فهي هندسه لا إقليديه هناك هندسات لا إقليديه عديده لكن ما يخص هذا البحث هي الهندسه التي كشفها كل من لوباتشفسكي و بولياني (Bolyai) وغاوس وتعرف هذه الهندسه، بالهندسه الهذلوليه أو الهندسه الزائديه Hyperbolic geometry أو هندسة لوباتشفسكي.
الهندسه الهذلوليه هي الهندسة المبنية على مسلمات الهندسة المحايدة (neutral geometry)، وتستبدل مسلمة هيلبرت في التوازي، بمسلمة التوازي في الهندسة الهذلوليه.
مسلمة التوازي في الهندسه الهذلوليه من نقطه P لا على المستقيم L على الأقل يمر مستقيمان من P يوازيان المستقيم L تسعى الهندسه المحايدة على إثبات القضايا الهندسية مستغنية عن مسلمة التوازي. مستعينة بالمسلمات الأربعة الأولى للهندسة الإقليديه، كمحاوله لفرز القضايا المعتمدة والغير معتمدة على مسلمة التوازي. مسلمات هيلبرت هي أكثر شمولية من مسلمات إقليدس وتظهر مسلمة التوازي في مسلمات هيلبرت بهذه الصيغة:
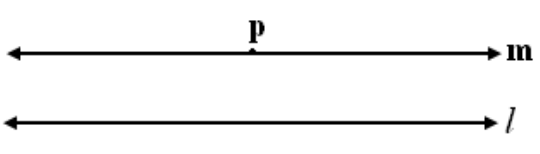
لكل مستقيم كالمستقيم L ولأي نقطه لا على المستقيم L كالنقطه P على الأكثر هناك مستقيم واحد هو m يمر من P ويوازي L.
في الهندسه الإقليديه لا يمكن تقسيم الزاوية بالفرجال والمسطره الغير مدرجه الى ثلاث زوايا متساويه، كذلك في الهندسه الهذلوليه هذا التقسيم غير ممكن، لا يمكن تقسيم قطعة مستقيم بهذا الشرط الى ثلاث أقسام متساويه في الهندسه الهذلوليه في الهندسه الإقليديه لا يمكن رسم مربع بالفرجال والمسطره الغير مدرجه مساحته تساوي مساحة دائرة معلومة، لكن هذا الرسم بهذا الشرط ممكن في الهندسه الهذلوليه.
العجيب في هذه الهندسه هو أمكانية وجود حدّ لمساحة المثلث فيها ولا حد لطول أضلاع هذا المثلث!
الاكثر قراءة في مواضيع عامة في النظرية النسبية
اخر الاخبار
اخبار العتبة العباسية المقدسة
