


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 10-11-2016
Date: 25-10-2016
Date: 1-11-2016
|
Space and Time Together
To explain Einstein’s 1905 special theory of relativity and Minkowski’s 1908 unification that combines three space dimensions and one time dimension into a four dimensional space-time continuum, most introductory physics textbooks use a four-dimensional coordinate system, with three real coordinates for space and one imaginary coordinate for the time coordinate. Why not four real coordinates? Why not have three imaginary space coordinates and one real-time coodinate?
Answer
Using three real spatial coordinates and one imaginary time coordinate for calculations works correctly when calculating the squares of space-time coordinates and their sums and differences. The important relationship is the space-time interval τ defined by τ2 = c2 Δt2 – Δx2 – Δy2 – Δz2, where the Δx’s are the four “distances.” However, physics textbooks that use an interval τ defined by τ2 = + Δx2 + Δy2 + Δz2 – c2 Δt2 are making a mathematical faux pas in choosing three real space coordinates and one imaginary time coordinate that is, the set (x, y, z, ict) with i being the imaginary and c being the speed of light instead of vice versa. Fortunately, this fundamental error does not affect the calculations of time intervals and spatial separations because these calculations involve the differences of squared quantities. To be mathematically correct in the (3 + 1)-dimensional spacetime, one must use quaternions, which are numbers in the form q = a + bi + cj + dk, with i, j, and k being 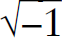 and a, b, c, and d being ordinary real numbers, because they are the numbers in four dimensions that properly handle rotations, translations, and Lorentz transformations. Today, quaternions are used everywhere in science to describe the dynamics of motion in three-space. Spinors are equivalent mathematical entities used in quantum mechanical wave functions to describe the electron and other fermions in (3 + 1)-D space.
and a, b, c, and d being ordinary real numbers, because they are the numbers in four dimensions that properly handle rotations, translations, and Lorentz transformations. Today, quaternions are used everywhere in science to describe the dynamics of motion in three-space. Spinors are equivalent mathematical entities used in quantum mechanical wave functions to describe the electron and other fermions in (3 + 1)-D space.
Quaternions were first “discovered” by W. R. Hamilton in the 1800s, and the quaternion q has one real component and three imaginary components. Just as complex numbers are formed from pairs of real numbers, quaternions are formed from pairs of complex numbers. Thus one should assign the time coordinate to the real component and the three space coordinates to the three imaginary components of a quaternion. Hence, mathematically, we live in a quaternion world with an imaginary 3-D physical space and a 1-D real-time clock!



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|