


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 9-8-2016
Date: 28-7-2016
Date: 11-8-2016
|
Rotating Hollow Hoop
A thin hollow cylindrical pipe is bent to form a hollow circular ring of mass m and radius R. The ring is attached by means of massless spokes to a vertical axis, around which it can rotate without friction in a horizontal plane. Inside the ring, a point mass P of mass m is free to move without friction, but is connected to a point H of the ring by a massless spring which exerts a force kΔs, where Δs is the length of the arc HP (see Figure 1.1). Take as variables the angles θ and φ of CH and CP with the x axis.
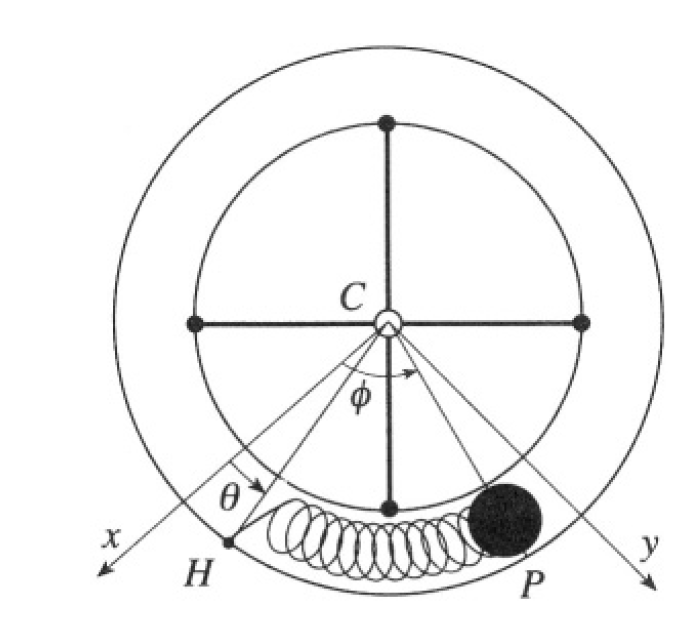
Figure 1.1
a) Write the Lagrangian and the Hamiltonian, and rewrite them in terms of the variables

b) Find an integral of motion other than the energy, and show that its Poisson bracket with H is zero.
c) Integrate the equations of motion with these initial conditions at t = 0:
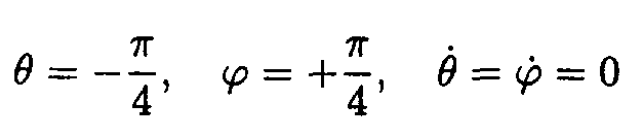
SOLUTION
The Lagrangian for the system shown in Figure 1.2 can be written in
the form
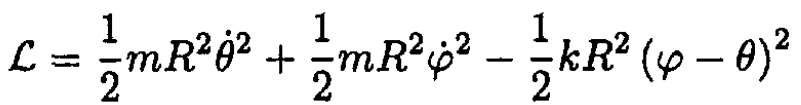
The generalized momenta are

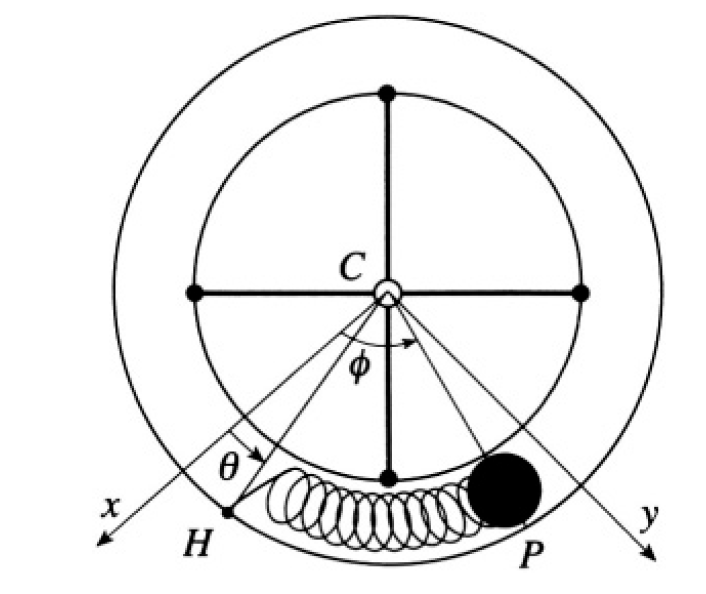
Figure 1.2
The Hamiltonian is
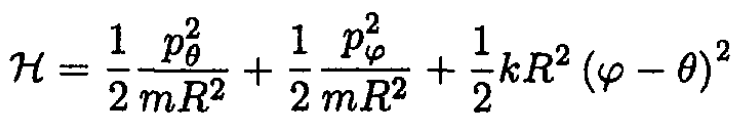
Changing the variables gives
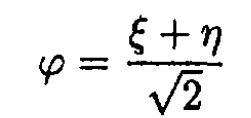 (1)
(1)
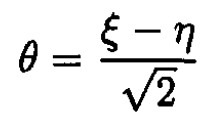 (2)
(2)
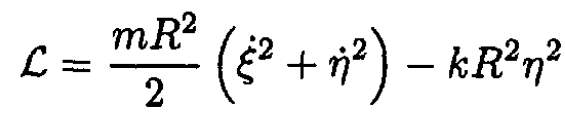 (3)
(3)
Again, the generalized momenta are
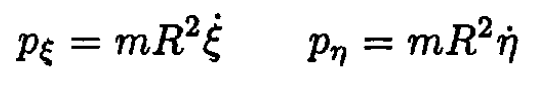
The Hamiltonian is
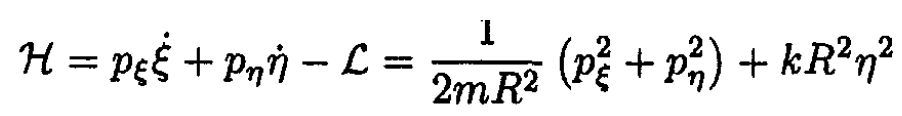
b) Since  we have
we have

The Poisson bracket of pζ with H is
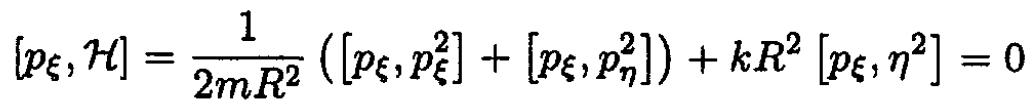
So, pζ is indeed the integral of motion since its Poisson bracket with H is equal to zero.
c) From (3), the equations of motion are
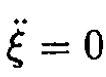 (4)
(4)
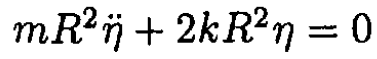 (5)
(5)
From (4) and (5) we obtain
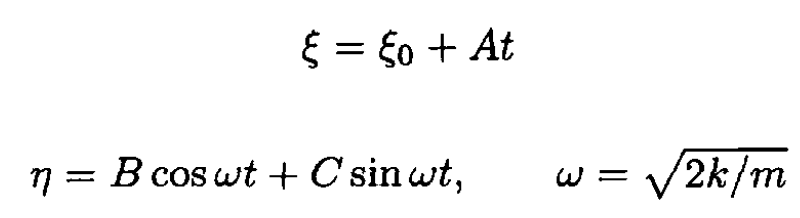
Using the initial conditions for (1) and (2) we have
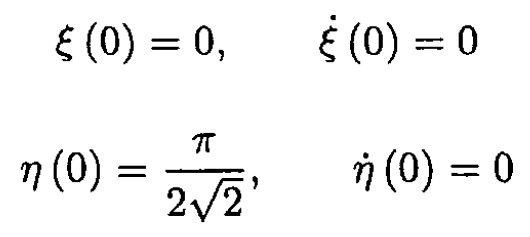
So
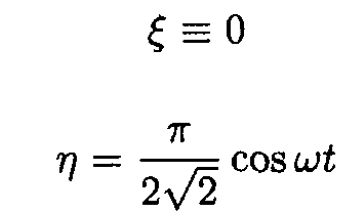
and finally
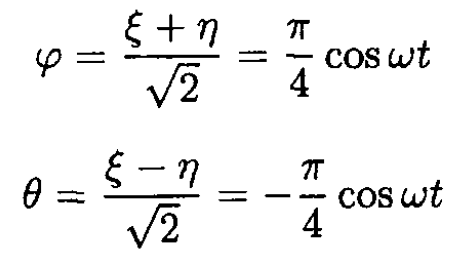



|
|
|
|
تحذير من "عادة" خلال تنظيف اللسان.. خطيرة على القلب
|
|
|
|
|
|
|
دراسة علمية تحذر من علاقات حب "اصطناعية" ؟!
|
|
|
|
|
|
|
العتبة العباسية المقدسة تحذّر من خطورة الحرب الثقافية والأخلاقية التي تستهدف المجتمع الإسلاميّ
|
|
|