Waves and Particles

As we have seen in the last section, there is good evidence that electromagnetic radiation, which, classically, is regarded as a wave motion, can also behave as a stream of particles-photons, The obvious question to ask is whether particles, such as electrons, can in turn exhibit wavelike properties. That this might be so was first conjectured by de Broglie in 1924. He noted that for a photon the energy is proportional to the frequency and, therefore, inversely proportional to the wavelength of the associated wave. Then, using a simple relationship between energy ( E ) and the magnitude of the momentum ( p ) arising in relativity theory (E = pc where c is the speed of light), he was able to deduce* a relation between the wavelength and the magnitude of the photon momentum, namely

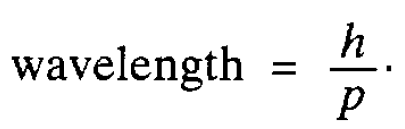
He suggested that this relationship might also hold for material particles as well as for photons, which are, of course, massless. It was important to test his idea experimentally and this was done for electrons by Davisson and Germer in 1927. One characteristic of waves is that they can be diffracted and they found (interestingly by accident!) that electrons accelerated through a potential difference and then striking a nickel crystal were scattered preferentially in certain directions. This indicated that diffraction was taking place and clearly the regular lines of atoms in the crystal were playing the role of the lines which are engraved on a diffraction grating used to diffract light. The spacing between the lines of atoms was known from the diffraction of x-rays by the crystal and, knowing this, the wave length of the ‘electron wave’ could be worked out. It agreed perfectly with de Broglie’s suggestion. Similar confirmatory experiments have now been carried out with other particles and even atoms. Thus wave particle duality was firmly established. However a fundamental question remained: what is the nature of the wave associated with a material particle? Waves encountered so far have referred to some physically measurable quantity such as the

*The energy of a photon is hv, which we now equate to pc (hv = pc). Its wavelength is given by c/v which, from the foregoing expression, is equal to h/p.

height of water, the density of air or the strength of electric and magnetic fields. What does the intensity of a ‘matter wave’ measure? The currently accepted interpretation was first suggested by Max Born following on detailed mathematical formulation of these quantum ideas by Heisenberg and Schrodinger. He interpreted the wave as carrying information about the location of the particle: its intensity at any point is simply a measure of the probability of finding the associated particle at that point. The particle is most likely to be found at positions where the wave is strong and least likely to be found where the wave is weak. Therefore the diffraction pattern of the wave associated with the electrons in the Davisson and Germer experiment had the equivalent of bright and dark areas obtained with the diffraction of light, but the ‘bright’ areas in the electron case are those where many electrons are detected, since the wave is intense there, and the ‘dark’ areas are those where few electrons are detected. This interpretation brings with it profound conceptual problems. Consider the example of a particle moving along in a straight line with a definite momentum. From the above relationship the associated wave has a definite wavelength. Such a wave, representing a moving particle, must be a travelling wave and therefore extends endlessly in space. This means that, although we know the momentum of the particle precisely we have no idea where it is since the wave telling us about the probability of finding it somewhere extends to infinity. Of course, in principle, we can know where a particle is by shining light on it and ‘looking’ at it. However, light is spread out it is a wave motion and so the best that could be done would be to localize the particle within one of the light’s wavelengths. This means that there is an uncertainty in its position of the order of one wavelength. Further, the light carries momentum equal to h divided by this wavelength as mentioned earlier, so that in bouncing off the particle momentum of that order of magnitude is given to the electron. There is, therefore, also an uncertainty of that amount in the momentum of the particle. To be more certain of the particle’s position would require a smaller wavelength which, in turn, would lead to a larger uncertainty in the momentum. Given that the uncertainty in the particle’s position is simply the wavelength of the light and that the uncertainty in its momentum is h divided by this wavelength, it follows at once that

(position uncertainty) × (momentum uncertainty) 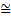 h

where, the reader is reminded, the symbol 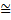 signifies ‘approximately equal’. It is used because the argument leading to this has been semiquantitative. The above expression is a statement of what is known as Heisenberg’s Uncertainty Relation. Clearly, as the momentum uncertainty approaches zero, then the position uncertainty approaches infinity (h divided by zero) as deduced earlier. Roughly speaking, if you know precisely where a particle is you cannot know what it is doing or, if you know precisely what it is doing, you cannot know where it is! Because of the small size of h this effect is also very small and only becomes significant at the atomic level; it has no importance in, for example, playing snooker. Indeed for entities much larger and heavier than atoms, such as snooker balls, quantum mechanics gives essentially the same results as classical Newtonian mechanics. Niels Bohr called this relationship between quantum and classical mechanics the correspondence principle. It must be stressed here that the relation does not reflect some clumsiness in our procedures for measuring things; it is intrinsic to the particle wave duality exhibited by material particles and electromagnetic radiation. It poses problems of interpretation and is still the subject of much debate. Consider, for example, the interference of light passing through two slits but treating the light as photons rather than waves. For a stream of photons the situation is straightforward in that the intensity of the waves relate simply to the probability of a photon being there. Thus there are many photons at the bright points of the interference pattern and few at the darker points. However consider just one of these photons arriving at the two slits. It can only go through one, so how does it ‘know’ that the other one is there and therefore participate in forming the interference pattern? The same question would arise if the experiment studied interference using a beam of electrons. There is no question of the photon or electron ‘splitting up’ and going through both slits; rather the associated wave goes through both slits and its intensity then determines the probability of the particle going through one or the other slit. This and many other similar questions have been written about extensively in much popular scientific literature.