The Greek philosopher Speusippus, who took over the running of the Academy from his uncle Plato, declared that the Pythagoreans believed that 10 had the right credentials for perfection. Why? Because the number of prime numbers between 1 and 10 (namely 2, 3, 5, 7) equalled the non-primes (4, 6, 8, 9) and this was the smallest number with this property. Some people have a strange idea of perfection.

It seems the Pythagoreans actually had a richer concept of a perfect number. The mathematical properties of perfect numbers were delineated by Euclid in the Elements and studied in depth by Nicomachus 400 years later, leading to amicable numbers and even sociable numbers. These categories were defined in terms of the relationships between them and their divisors. At some point they came up with the theory of superabundant and deficient numbers and this led them to their concept of perfection.

Whether a number is superabundant is determined by its divisors and makes a play on the connection between multiplication and addition. Take the number 30 and consider its divisors, that is all the numbers which divide into it exactly and which are less than 30. For such a small number as 30 we can see the divisors are 1, 2, 3, 5, 6, 10 and 15. Totalling up these divisors we get 42. The number 30 is superabundant because the addition of its divisors (42) is bigger than the number 30 itself.

The first few perfect numbers

A number is deficient if the opposite is true – if the sum of its divisors is less than itself. So the number 26 is deficient because its divisors 1, 2 and 13 add up to only 16, which is less than 26. Prime numbers are very deficient because the sum of their divisors is always just 1.

A number that is neither superabundant nor deficient is perfect. The addition of the divisors of a perfect number equal the number itself. The first perfect number is 6. Its divisors are 1, 2, 3 and when we add them up, we get 6. The Pythagoreans were so enchanted with the number 6 and the way its parts fitted together that they called it ‘marriage, health and beauty’. There is another story connected with 6 told by St Augustine (354–430). He believed that the perfection of 6 existed before the world came into existence and that the world was created in 6 days because the number was perfect.

The next perfect number is 28. Its divisors are 1, 2, 4, 7 and 14 and, when we add them up, we get 28. These first two perfect numbers, 6 and 28, are rather special in perfect number lore for it can be proved that every even perfect number ends in a 6 or a 28. After 28, you have wait until 496 for the next perfect number. It is easy to check it really is the sum of its divisors: 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 +248. For the next perfect numbers we have to start going into the numerical stratosphere. The first five were known in the 16th century, but we still don’t know if there is a largest one, or whether they go marching on without limit. The balance of opinion suggests that they, like the primes, go on for ever.

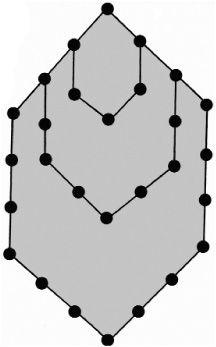
The Pythagoreans were keen on geometrical connections. If we have a perfect number of beads, they can be arranged around a hexagonal necklace. In the case of 6 this is the simple hexagon with beads placed at its corners, but for higher perfect numbers we have to add in smaller subnecklaces within the large one.

Mersenne numbers

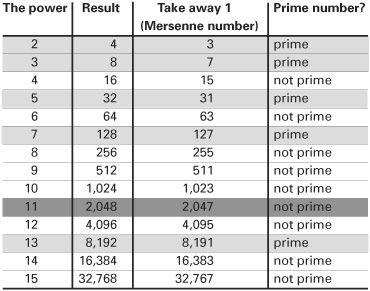
The key to constructing perfect numbers is a collection of numbers named after Father Marin Mersenne, a French monk who studied at a Jesuit college with René Descartes. Both men were interested in finding perfect numbers. Mersenne numbers are constructed from powers of 2, the doubling numbers 2, 4, 8, 16, 32, 64, 128, 256, . . ., and then subtracting a single 1. A Mersenne number is a number of the form 2ⁿ − 1. While they are always odd, they are not always prime. But it is those Mersenne numbers that are also prime that can be used to construct perfect numbers.

Mersenne knew that if the power was not a prime number, then the Mersenne number could not be a prime number either, accounting for the non-prime powers 4, 6, 8, 9, 10, 12, 14 and 15 in the table. The Mersenne numbers could only be prime if the power was a prime number, but was that enough? For the first few cases, we do get 3, 7, 31 and 127, all of which are prime. So is it generally true that a Mersenne number formed with a prime power should be prime as well?

Many mathematicians of the ancient world up to about the year 1500 thought this was the case. But primes are not constrained by simplicity, and it was found that for the power 11 (a prime number), 2¹¹ – 1 = 2047 = 23 × 89 and consequently it is not a prime number. There seems to be no rule. The Mersenne numbers 2¹⁷ – 1 and 2¹⁹ – 1 are both primes, but 2²³ – 1 is not a prime, because

Just good friends

The hard-headed mathematician is not usually given to the mystique of numbers but numerology is not yet dead. The amicable numbers came after the perfect numbers though they may have been known to the Pythagoreans. Later they became useful in compiling romantic horoscopes where their mathematical properties translated themselves into the nature of the ethereal bond. The two numbers 220 and 284 are amicable numbers. Why so? Well, the divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110 and if you add them up you get 284. You’ve guessed it. If you figure out the divisors of 284 and add them up, you get 220. That’s true friendship.

Mersenne Primes

Finding Mersenne primes is not easy. Many mathematicians over the centuries have added to the list, which has a chequered history built on a combination of error and correctness. The great Leonhard Euler contributed the eighth Mersenne prime, 2³¹ – 1 = 2,147,483,647, in 1732. Finding the 23rd Mersenne prime, 2¹¹²¹³ – 1, in 1963 was a source of pride for the mathematics department at the University of Illinois, who announced it to the world on their university postage stamp. But with powerful computers the Mersenne prime industry had moved on and in the late 1970s high school students Laura Nickel and Landon Noll jointly discovered the 25th Mersenne prime, and Noll the 26th Mersenne prime. To date 45 Mersenne primes have been discovered.

2²³ – 1 = 8,388,607 = 47 × 178,481

Construction work

A combination of Euclid and Euler’s work provides a formula which enables even perfect numbers to be generated: n is an even perfect number if and only if n = 2^p – 1(2^p – 1) where 2^p – 1 is a Mersenne prime.

For example, 6 = 2¹(2² – 1), 28 = 2²(2³ – 1) and 496 = 2⁴(2⁵ – 1). This formula for calculating even perfect numbers means we can generate them if we can find Mersenne primes. The perfect numbers have challenged both people and machines and will continue to do so in a way which earlier practitioners had not envisaged. Writing at the beginning of the 19th century, the table maker Peter Barlow thought that no one would go beyond the calculation of Euler’s perfect number

2³⁰(2³¹ – 1) = 2,305,843,008,139,952,128

as there was little point. He could not foresee the power of modern computers or mathematicians’ insatiable need to meet new challenges.

Odd perfect numbers

No one knows if an odd perfect number will ever be found. Descartes did not think so but experts can be wrong. The English mathematician James Joseph Sylvester declared the existence of an odd perfect number ‘would be little short of a miracle’ because it would have to satisfy so many conditions. It’s little surprise Sylvester was dubious. It is one of the oldest problems in mathematics, but if an odd perfect number does exist quite a lot is already known about it. It would need to have at least 8 distinct prime divisors, one of which is greater than a million, while it would have to be at least 300 digits long.

the condensed idea

The mystique of numbers