
Pseudoconvex Function
 المؤلف:
Borwein, J. and Lewis, A.
المؤلف:
Borwein, J. and Lewis, A.
 المصدر:
Convex Analysis and Nonlinear Optimization: Theory and Examples. New York: Springer Science+Business Media, 2006.
المصدر:
Convex Analysis and Nonlinear Optimization: Theory and Examples. New York: Springer Science+Business Media, 2006.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-7-2021
25-7-2021
 1933
1933
Pseudoconvex Function
Given a subset 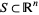 and a real function
and a real function 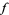 which is Gâteaux differentiable at a point
which is Gâteaux differentiable at a point 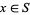 ,
, 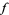 is said to be pseudoconvex at
is said to be pseudoconvex at  if
if
Here, 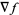 denotes the usual gradient of
denotes the usual gradient of 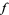 .
.
The term pseudoconvex is used to describe the fact that such functions share many properties of convex functions, particularly with regards to derivative properties and finding local extrema. Note, however, that pseudoconvexity is strictly weaker than convexity as every convex function is pseudoconvex though one easily checks that 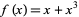 is pseudoconvex and non-convex.
is pseudoconvex and non-convex.
Similarly, every pseudoconvex function is quasi-convex, though the function 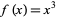 is quasi-convex and not pseudoconvex.
is quasi-convex and not pseudoconvex.
A function 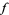 for which
for which 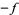 is pseudoconvex is said to be pseudoconcave.
is pseudoconvex is said to be pseudoconcave.
REFERENCES:
Borwein, J. and Lewis, A. Convex Analysis and Nonlinear Optimization: Theory and Examples. New York: Springer Science+Business Media, 2006.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


