

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Golden rectangles
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
67-72
23-2-2016
2372
Rectangles are all around us – buildings, photographs, windows, doors, even this book. Rectangles are present within the artists’ community – Piet Mondrian, Ben Nicholson and others, who progressed to abstraction, all used one sort or another. So which is the most beautiful of all? Is it a long thin ‘Giacometti rectangle’ or one that is almost a square? Or is it a rectangle in between these extremes?
Does the question even make sense? Some think so, and believe particular rectangles are more ‘ideal’ than others. Of these, perhaps the golden rectangle has found greatest favour. Amongst all the rectangles one could choose for their different proportions – for that is what it comes down to – the golden rectangle is a very special one which has inspired artists, architects and mathematicians. Let’s look at some other rectangles first.
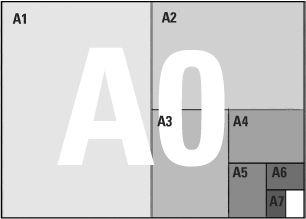
Mathematical paper
If we take a piece of A4 paper, whose dimensions are a short side of 210 mm and a long side of 297 mm, the length-to-width ratio will be 297/210 which is approximately 1.4142. For any international A-size paper with short side equal to b, the longer side will always be 1.4142 × b. So for A4, b = 210 mm, while for A5, b = 148 mm. The A-formulae system used for paper sizes has a highly desirable property, one that does not occur for arbitrary paper sizes. If an A-size piece of paper is folded about the middle, the two smaller rectangles formed are directly in proportion to the larger rectangle. They are two smaller versions of the same rectangle.
In this way, a piece of A4 folded into two pieces generates two pieces of A5. Similarly a piece of A5-size paper generates two pieces of A6. In the other direction, a sheet of A3 paper is made up of two pieces of A4. The smaller the number on the A-size the larger the piece of paper. How did we know that the particular number 1.4142 would do the trick? Let’s fold a rectangle, but this time let’s make it one where we don’t know the length of its longer side. If we take the breadth of a rectangle to be 1 and we write the length of the longer side as x, then the length-to-width ratio is x/1. If we now fold the rectangle, the length-to-width ratio of the smaller rectangle is 1/½x, which is the same as 2/x. The point of A sizes is that our two ratios must stand for the same proportion, so we get an equation x/1 = 2/x or x2 = 2. The true value of x is therefore √2 which is approximately by 1.4142.
Mathematical gold
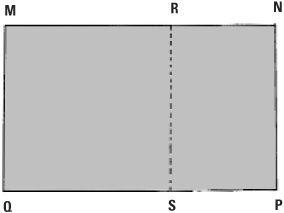
The golden rectangle is different, but only slightly different. This time the rectangle is folded along the line RS in the diagram so that the points MRSQ make up the corners of a square.
The key property of the golden rectangle is that the rectangle left over, RNPS, is proportional to the large rectangle – what is left over should be a mini-replica of the large rectangle.
As before, we’ll say the breadth MQ = MR of the large rectangle is 1 unit of length while we’ll write the length of the longer side MN as x. The length-to-width ratio is again x/1. This time the breadth of the smaller rectangle RNPS is MN – MR, which is x− 1 so the length-to-width ratio of this rectangle is 1/(x – 1). By equating them, we get the equation
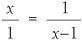
which can be multiplied out to give x2 = x + 1. An approximate solution is 1.618. We can easily check this. If you type 1.618 into a calculator and multiply it by itself you get 2.618 which is the same as x + 1 = 2.618. This number is the famous golden ratio and is designated by the Greek letter phi, Φ. Its definition and approximation is given by and this number is related to the Fibonacci sequence and the rabbit problem.
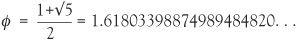
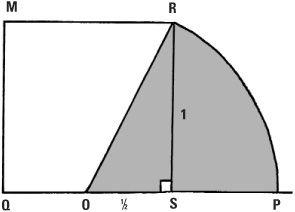
Going for gold
Now let’s see if we can build a golden rectangle. We’ll begin with our square MQSR with sides equal to 1 unit and mark the midpoint of QS as O. The length OS = ½, and so by Pythagoras’s theorem in the triangle ORS, OR = 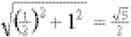
Using a pair of compasses centred on O, we can draw the arc RP and we’ll find that OP = OR = √5/2 . So we end up with
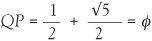
which is what we wanted: the ‘golden section’ or the side of the golden rectangle.
History
Much is claimed of the golden ratio Φ. Once its appealing mathematical properties are realized it is possible to see it in unexpected places, even in places where it is not. More than this is the danger of claiming the golden ratio was there before the artefact – that musicians, architects and artists had it in mind at the point of creation. This foible is termed ‘golden numberism’. The progress from numbers to general statements without other evidence is a dangerous argument to make.
Take the Parthenon in Athens. At its time of construction the golden ratio was certainly known but this does not mean that the Parthenon was based on it. Sure, in the front view of the Parthenon the ratio of the width to the height (including the triangular pediment) is 1.74 which is close to 1.618, but is it close enough to claim the golden ratio as a motivation? Some argue that the pediment should be left out of the calculation, and if this is done, the width-to-height ratio is actually the whole number 3.
In his 1509 book De divina proportione, Luca Pacioli ‘discovered’ connections between characteristics of God and properties of the proportion determined by Φ. He christened it the ‘divine proportion’. Pacioli was a Franciscan monk who wrote influential books on mathematics. By some he is regarded as the ‘father of accounting’ because he popularized the double-entry method of accounting used by Venetian merchants. His other claim to fame is that he taught mathematics to Leonardo da Vinci. In the Renaissance, the golden section achieved near mystical status – the astronomer Johannes Kepler described it as a mathematical ‘precious jewel’. Later, Gustav Fechner, a German experimental psychologist, made thousands of measurements of rectangular shapes (playing cards, books, windows) and found the most commonly occurring ratio of their sides was close to Φ.
Le Corbusier was fascinated by the rectangle as a central element in architectural design and by the golden rectangle in particular. He placed great emphasis on harmony and order and found this in mathematics. He saw architecture through the eyes of a mathematician. One of his planks was the ‘modulator’ system, a theory of proportions. In effect this was a way of generating streams of golden rectangles, shapes he used in his designs. Le Corbusier was inspired by Leonardo da Vinci who, in turn, had taken careful notes on the Roman architect Vitruvius, who set store by the proportions found in the human figure.
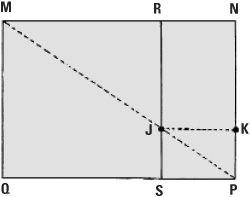
Other shapes
There is also a ‘supergolden rectangle’ whose construction has similarities with the way the golden rectangle is constructed.
This is how we build the supergolden rectangle MQPN. As before, MQSR is a square whose side is of length 1. Join the diagonal MP and mark the intersection on RS as the point J. Then make a line JK that’s parallel to RN with K on NP. We’ll say the length RJ is y and the length MN is x. For any rectangle, RJ/MR = NP/MN (because triangles MRJ and MNP are similar), so y/1 = 1/x which means x × y = 1 and we say x and y are each other’s ‘reciprocal’. We get the supergolden rectangle by making the rectangle RJKN proportional to the original rectangle MQPN, that is y/(x− 1) = x/1. Using the fact that xy = 1, we can conclude that the length of the supergolden rectangle x is found by solving the ‘cubic’ equation x3 = x2 + 1, which is clearly similar to the equation x2 = x + 1 (the equation that determines the golden rectangle). The cubic equation has one positive real solution ψ (replacing x with the more standard symbol Φ) whose value is
ψ = 1.46557123187676802665. . .
the number associated with the cattle sequence .Whereas the golden rectangle can be constructed by a straight edge and a pair of compasses, the supergolden rectangle cannot be made this way.
the condensed idea
Divine proportions

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















