Algebra tiles are used to model integers and variables to aid in learning addition, subtraction, multiplication, and division of positive and negative values. Algebra tiles are especially useful in modeling multiplication and division because their dimensions are based on the concept of area.

They can be bought or made, and they usually consist of three shapes: small squares for integers, rectangles for the variable x, and slightly longer rectangles for the variable  y. The widths of the tiles for integers, for  x, and for  y  are the same: one unit. Notice that the length of the  x-tile is unknown: it is  not equal to a certain number of unit tiles. The positive tiles are one color, and the negative tiles are another color, as shown in Figure 1(a).

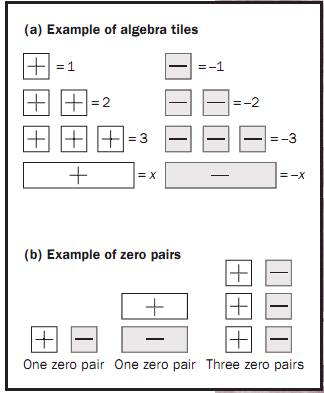
Figure 1. Examples ofalgebra tiles and zero pairs.

One positive integer and one negative integer make a zero pair, as shown in Figure 1b. Because adding or subtracting zero does not change a number  (e.g., 8+ 0 = 8), zero pairs will be the basis of simplifying expressions.

Addition, Subtraction, Multiplication, and Division  with Algebra Tiles

Addition is the simplest operation to do with algebra tiles. Just draw tiles for each term and then cross out zero pairs until no zero pairs remain. The total number of tiles that are left over is the answer, as shown in examples (a) through (c) of Figure 2.

Addition and subtraction are opposites. Whereas the strategy for addition is to remove zero pairs, the strategy for subtraction is to insert zero pairs. To subtract, start by drawing tiles for the first term, and then take away the amount to be subtracted, as shown in examples (d) through (g) of Figure 2.

If a closet measures 3 feet by 4 feet, then one might quickly sketch a rectangle with sides measuring 3 units and 4 units. Multiplication with algebra tiles uses the same concept. The length and width are the factors, and the area is the product. Recall the rules for multiplying positive and negative numbers: if the signs of the factors are the same, the product is positive; if the signs are different, the product is negative.

To model the product 3 x 4 using algebra tiles, start with an off-center “t” as a guideline, as shown in Figure 3(a). Place the factors three and four in the upper right and lower left portions of the “t.” Draw the edges of a 3-by-4 rectangle in the lower right portion of the “t.” Then extend the sides of each algebra tile across and down the rectangle. Count the number of resulting integer squares inside the rectangle to find the answer. In this ex-

ample, the answer is 12. Examples (b) through (d) show other multiplication problems.

Figure 2. Examples of addition and subtraction using algebra tiles.

Division with algebra tiles employs the idea of division as sharing. Start by drawing the first term, and then divide its tiles into piles of equal amounts.

The amount in one pile is the answer. See examples (e) and (f ) in Figure 3.

Other Ways to Model Mathematics

Another conceptual way to represent integers and variables is to use cups and counters. Cups represent variables, and counters represent integers. Like algebra tiles, one color is used for positives, and another color is used for negatives. Cups are a great way to represent variables because, like a cup, variables

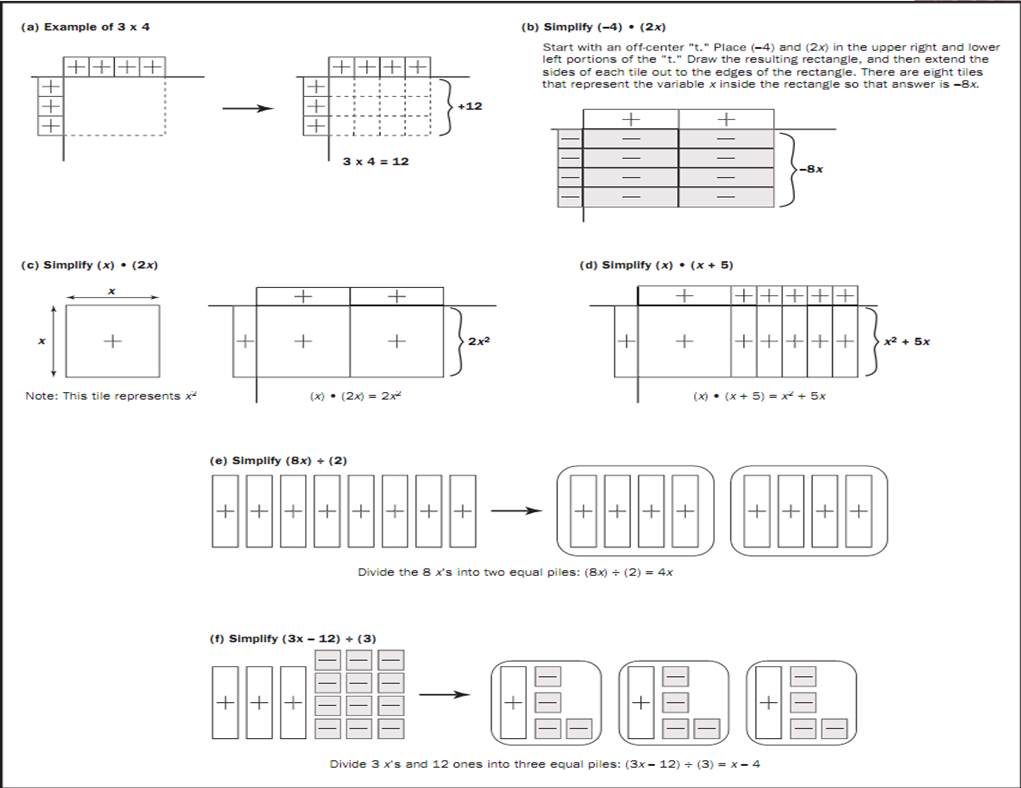
Figure 3. Examples of multiplication and division using algebra tiles.

can hold one, many, or no values. Geoboards, blocks, and even household items can be used to model proportions, slope, patterns, and functions.

The following example uses patterns of blocks to model building a tunnel. A student has built a tunnel using blocks. The height of the tunnel is two blocks, and the width of the tunnel is one block. See the drawings below. If the tunnel has one layer of thickness in all directions, then it will require seven blocks to build it; if it has two layers of thickness, then it will require eighteen blocks to build it, and so on. A table can be made to show how many cubes are required to make tunnels of different thicknesses.

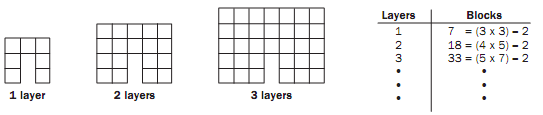
By studying the blocks and the table of relationships between layers and blocks, a pattern can be seen. For one layer, the tunnel requires enough blocks to make a 3 x 3 square less two blocks. For two layers, it requires enough blocks to make a 4x 5 rectangle less two blocks. For three layers,  it requires enough blocks to make a 5 x 7 rectangle less two blocks.

To predict the number of blocks required for x layers, a function can be written in which y is the number of blocks required for a particular number of layers, x. The equation can be written as y = [(x + 2)(2x + 1)] - 2.

The number of blocks needed for four layers is y = (4 + 2)(8 + 1) - 2 = 52. This prediction follows the pattern in the table. For ninety-eight layers,  19,698 blocks are required. This example with blocks shows that any pattern made with models can be studied to try to write a function and make predictions.

_________________________________________________________________________________________________________

Reference

Amdahl, Kenn, and Jim Loats. Algebra Unplugged. Broomfield, CO: Clearwater Publishing Co., 1995.