المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | محل هندسي Locus |
 5797
 09:30 صباحاً
التاريخ: 9-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 299|
أقرأ أيضاً
التاريخ: 29-12-2015
1804
التاريخ: 9-11-2015
2132
التاريخ: 13-12-2015
3375
التاريخ: 16-12-2015
1058
|
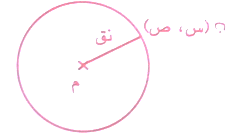
هو مسار نقطة متحركة في المستوى لرسم منحني تحت شروط معينة , إذ تنتج هذه المسارات أشكالاً هندسية معروفة في الرياضيات , فالدائرة مثلاً بلغة المحل الهندسي : هي مسار نقطة متحركة في مستوى شرط ان يكون بعدها عن نقطة اخرى ثابتة ( تسمى المركز م ) بعداً معلوماً دائماً ، هذا البعد يسمى نصف قطر الدائرة , كما في الشكل حيث النقطة ن (س ، ص) متحركة فترسم منحني يسمى الدائرة.
|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|
