المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | الفضاء Space |
 1082
 08:50 صباحاً
التاريخ: 22-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 221-222|
أقرأ أيضاً
التاريخ: 9-12-2015
10758
التاريخ: 5-11-2015
808
التاريخ: 3-12-2015
1382
التاريخ: 29-12-2015
3526
|
الفضاء كمفهوم في الرياضيات هو مجموعة غير منتهية من النقط , يحتوي المستقيمات والمستويات ويجسد المجسمات ذا الثلاثة أبعاد مركز اهتمام الهندسة الفضائية .
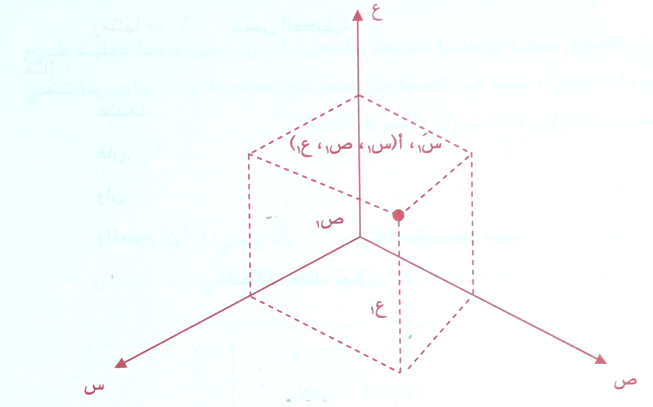
هذا ويممكن تعميم نظام الإحداثيات الديكارتية لتمثيل النقاط في الفضاء باستخدام ثلاثة مستقيمات متعامدة تتقاطع في نقطة واحدة تسمى نقطة الأصل م(0 ، 0 ، 0) كما في الشكل الذي يوضح موقع النقطة أ (س1 ، ص1 ، ع1) في الفضاء .
وكما تلاحظ فإن النقطة أ تمثل موضع رأس المكعب المنقط وكأنه المعلق بالفضاء .
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
